Documentación xgboost
Datos de ejemplo
En este documento se muestra cómo implementar el algoritmo XGBoost con R a través de la biblioteca que lleva el mismo nombre y haciendo uso del tidymodels. Para ejemplificar el ajuste de modelos de clasificación se obtuvieron datos de ejemplo aplicado en ciencias animales, específicamente en la detección de patrones de infección de mastitis en vacas.
Detección de mastitis
Requisitos previos
- Para replicar este documento es necesario instalar las siguientes bibliotecas:
-
tidyverse: manipulación y visualización de datos. -
readxl: lectura de datos en formato de Excel. -
janitor: manipulación de datos. -
visdat: análisis exploratorio de datos. -
tidymodels: entrenamiento y evaluación de modelos de machine learning. -
xgboost: algoritmoxgboost. -
doParallel: procesamiento en paralelo (cómputo distribuido). -
parallelprocesamiento en paralelo (cómputo distribuido). -
vip: calcular importancia de variables. -
ggsci: paletas de colores. -
ggforcecomplemento para gráficos. -
FactoMineR: análisis multivariado. -
knitr: presentación de tablas (data.frame).
-
- Descargar los datos para ejemplo:
-
Nota: es importante mencionar que cuando cargamos la meta-biblioteca
tidymodelsse activan otras bibliotecas que usaremos más adelante.
Bibliotecas
Tema para ggplot2
Código
mi_temagg <- theme_minimal() +
theme(axis.text.x = element_text(color = "black"),
axis.text.y = element_text(color = "black"),
strip.background = element_rect(fill = "gray5"),
strip.text = element_text(color = "white", size = 12),
legend.position = "top")
theme_set(mi_temagg)Detección de mastitis
- La variable respuesta está identificada como
diagnosis. En principio tiene 4 niveles, sin embargo, para el ejemplo fueron filtrados sólo los nivelesEDP(transmisión en el período seco - sin lactancia) yEL(transmisión en período de lactancia). - La base de datos consta de 1000 observaciones y 229 variables, es decir, que existen 228 variables predictoras. Cuando se aplicó el filtro quedaron 914 observaciones.
Base de datos
Código
| diagnosis | quarter_dates_q0 | no_recordings_q0 | l_1_q0_bmscc_000_cells_ml | l_1_q0_percent_chronic | l_1_q0_percent_200k |
|---|---|---|---|---|---|
| EDP | 06/10/2009 | 0 | 0 | 0.0 | 0.0 |
| EDP | 06/12/2009 | 3 | 284 | 27.8 | 40.6 |
| EL | 20/04/2012 | 0 | 0 | 0.0 | 0.0 |
| EL | 16/07/2009 | 3 | 222 | 21.1 | 26.3 |
| EL | 16/10/2013 | 3 | 251 | 27.5 | 34.3 |
| EDP | 12/01/2013 | 3 | 154 | 12.3 | 17.0 |
Análisis exploratorio
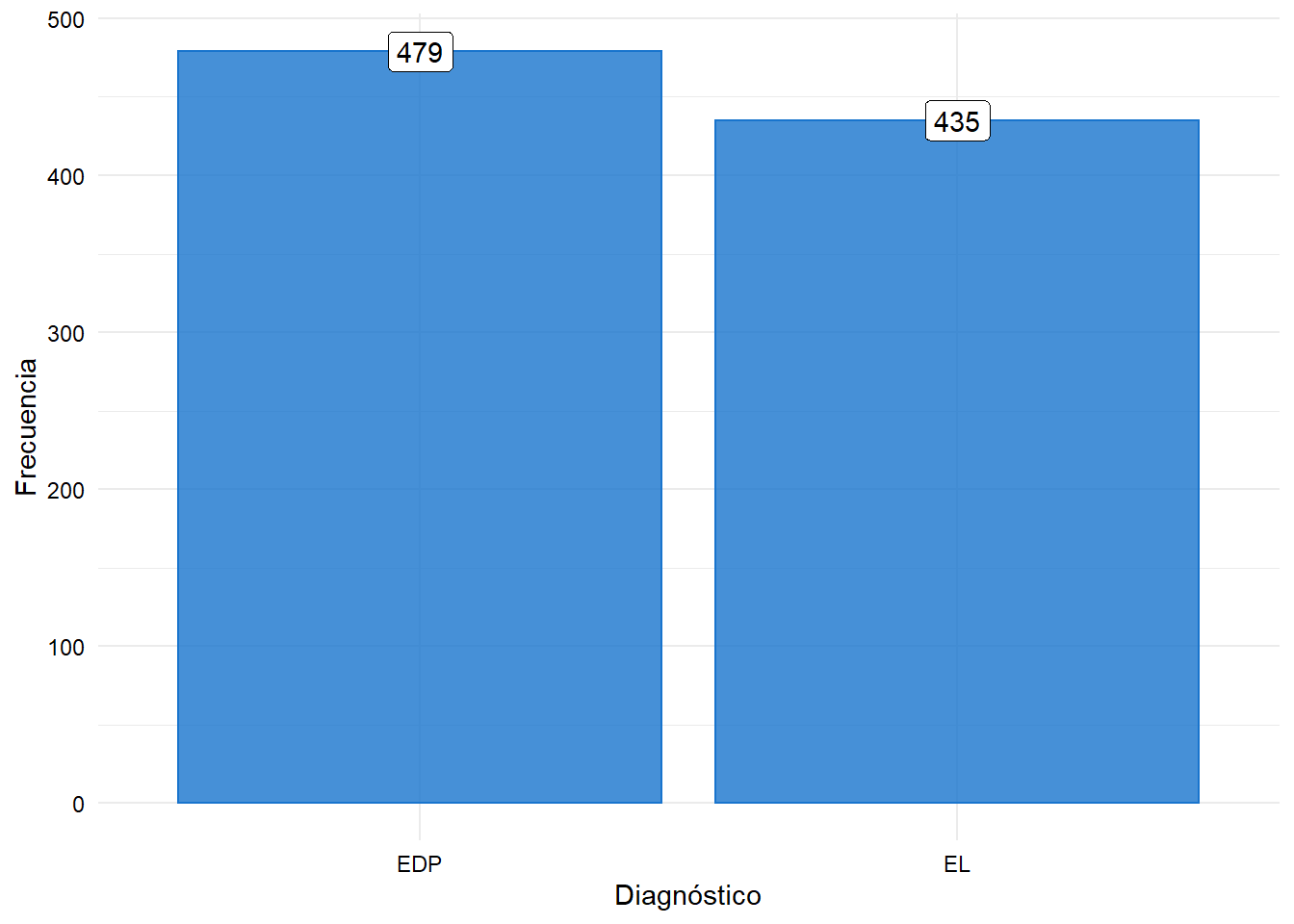
- Frecuencia absoluta para niveles de la variable respuesta.
Código
- Distribuciones de algunas variables numéricas: como el número de variables es alto, selecciono al azar 8 de ellas para construir el gráfico.
Código
# Números al azar
set.seed(1992)
variables_azar <- sample(x = 228, size = 8, replace = FALSE)
mastitis %>%
select(diagnosis, variables_azar) %>%
pivot_longer(cols = -diagnosis) %>%
ggplot(aes(x = value, fill = diagnosis, color = diagnosis)) +
facet_wrap(~name, scales = "free", ncol = 4) +
geom_density(alpha = 0.8) +
scale_x_log10() +
scale_color_jama() +
scale_fill_jama() +
labs(x = "", y = "Densidad", color = "Diagnóstico",
fill = "Diagnóstico")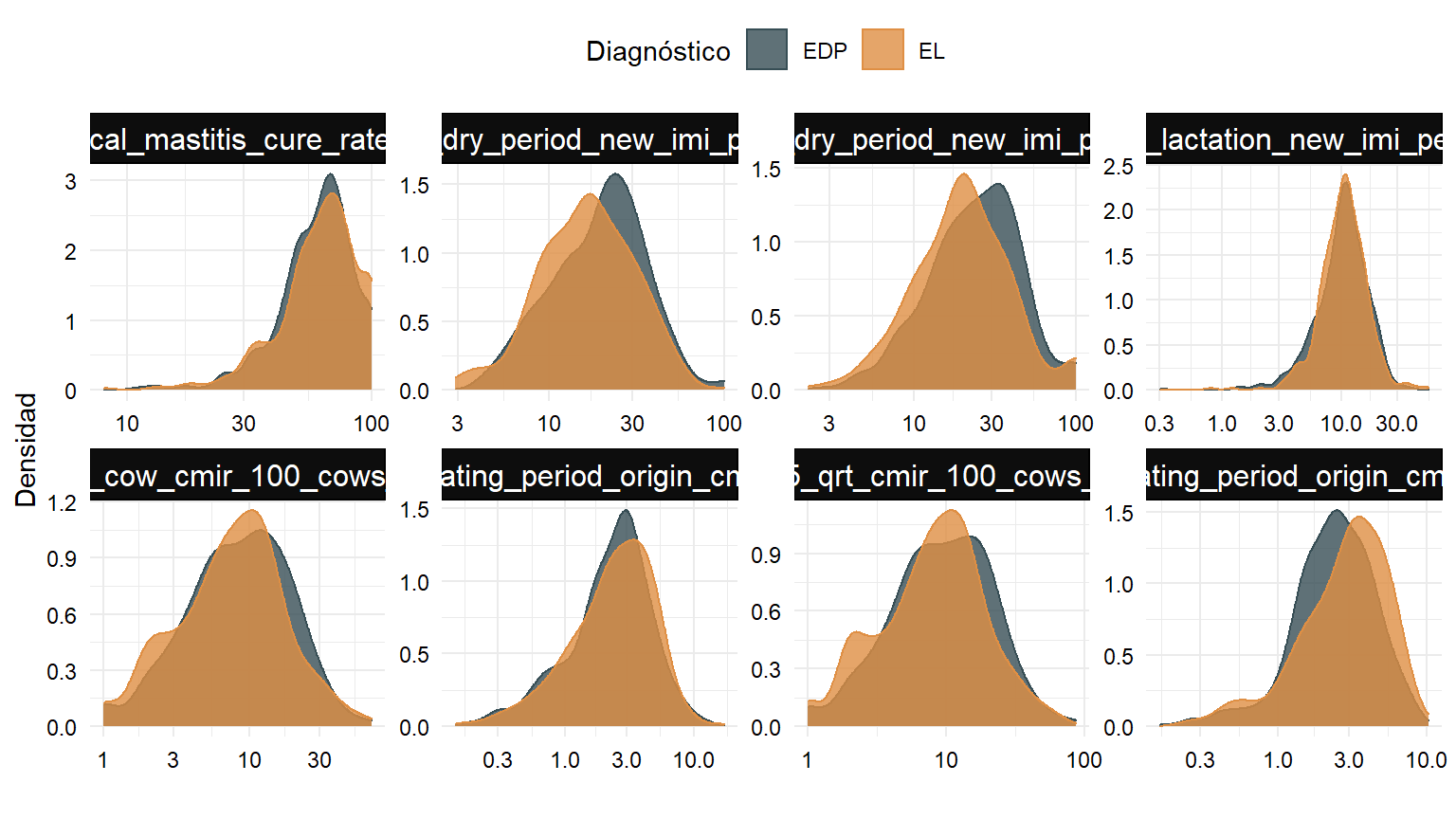
- Verificamos si existen valores ausentes. Se observan algunas filas con valores
NA.
Código
vis_miss(mastitis)
- Con la finalidad de evidenciar si existe algún patrón de asociación subyacente en el total de variables, se realizó análisis de componentes principales y se grafican los dos primeros componentes. No existe algún comportamiento de agrupación al reducir la dimensión a los dos primeros componentes. Se observó que la retención de variabilidad de estas dos coordenadas apenas alcanzó el 30% aproximadamente.
Código
# Análisis de componentes principales
datos_pca <- mastitis
pca <- PCA(X = datos_pca %>%
select(where(is.numeric)),
scale.unit = TRUE,
graph = FALSE)
# Agregando componentes a la base de datos
datos_pca$cp1 <- pca$ind$coord[, 1]
datos_pca$cp2 <- pca$ind$coord[, 2]
# Gráfico de las 2 primeras componentes
datos_pca %>%
ggplot(aes(x = cp1, y = cp2, color = diagnosis)) +
geom_point() +
geom_hline(yintercept = 0, color = "black", linetype = 2) +
geom_vline(xintercept = 0, color = "black", linetype = 2) +
scale_color_jama() +
labs(x = "CP1 (15.74 %)", y = "CP2 (14.09 %)", color = "Diagnóstico")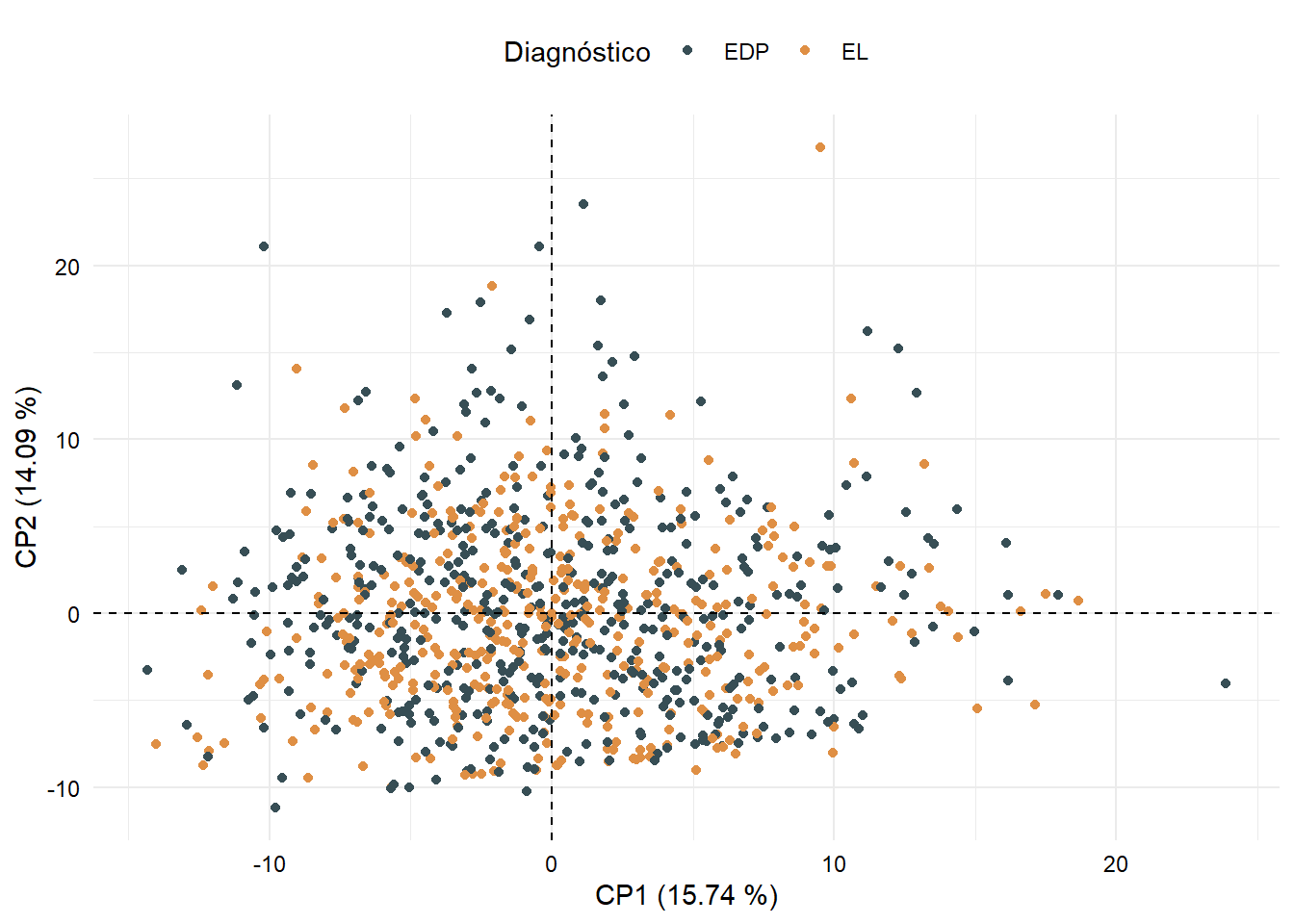
- Los resultados exploratorios sugieren cuatro cosas importantes:
- El problema de clasificación bajo análisis podría ser denominado de clases balanceadas, ya que las frecuencias absolutas son similares para cada nivel a predecir.
- Algunas variables predictoras no tienen comportamiento gaussiano. Parte de la estrategia del análisis, en estos casos, podría ser la implementación de algún tipo de transformación previo al entrenamiento de los modelos, no obstante, este paso no se aplicará dada la robustez que presenta el algoritmo XGBoost frente a distribuciones asimétricas.
- Existen observaciones con valores ausentes para una o más variables. Algunos algoritmos como la regresión logística o los bosques aleatorios, no permiten la inclusión de valores
NAal entrenar los modelos, sin embargo, con XGBoost no existe este inconveniente, puesto que soporta valores vacíos. - El análisis de componentes principales no muestra alguna tendencia de agrupación entre las clases evaluadas. La retención de variabilidad de las tres primeras componentes no supera el 50%, resultado que podría sugerir que las relaciones de tipo lineal no son plausibles en este conjunto de datos.
Train y Test
- En este ejemplo los datos fueron divididos en train y test con proporciones de 80 y 20 %, respectivamente. Se utiliza muestreo estratificado en función de la variable respuesta. Se eliminaron 4 variables que tienen información de fechas; aunque podrían ser tratadas de alguna manera especial, en este caso no fueron tenidas en cuenta.
- La biblioteca
rsamplepermite realizar la división.
Código
# Variables fechas
variables_fechas <- mastitis %>%
select(is.character, -diagnosis) %>%
names()
# Datos para modelos
data_modelos <- mastitis %>% select(-variables_fechas)
set.seed(1992)
particiones <- initial_split(data = data_modelos, prop = 0.80, strata = diagnosis)
train <- training(particiones)
test <- testing(particiones)- Podemos ver el objeto
particionesque proporciona información de la partición de datos. Los modelos son entrenados con 733 observaciones y con 181 se evalúa el desempeño de los mismos.
Código
particiones<Training/Testing/Total>
<731/183/914>Validación cruzada
- Se utiliza validación cruzada k-fold con \(k = 10\).
- La biblioteca
rsamplepermite configurar diferentes métodos de validación cruzada.
Código
set.seed(1992)
config_cv <- vfold_cv(data = train, v = 10)Preprocesamiento
- En este ejemplo no se hará énfasis en las estrategias de preprocesamiento o ingeniería de características, sin embargo, serán comparados algoritmos con imputación de valores ausentes (con método k vecinos más cercanos) respecto a algoritmos sin imputación.
- La biblioteca
recipespermite realizar múltiples tareas de preprocesamiento e ingeniería de características.
Código
no_impute <- recipe(diagnosis ~ ., data = train)
si_impute <- recipe(diagnosis ~ ., data = train) %>%
step_impute_knn(all_predictors())Modelo XGBoost
- El algoritmo XGboost tiene múltiples hiperparámetros que pueden ser sintonizados, sin embargo, en este ejemplo sólo ser hará tuning sobre los siguientes:
-
mtry: número de predictores que se muestrearán aleatoriamente en cada división al crear los modelos. -
min_n: número mínimo de observaciones requeridas en un nodo para que se produzca la división. -
tree_depth: profundidad máxima del árbol (número de divisiones).
-
- El número de árboles (
trees) se estableció en 1000. - La tasa de aprendizaje (
learn_rate) se estableció en 0.1. - La proporción de observaciones muestreadas (
sample_size) en cada rutina de ajuste se estableció en 0.8. - Los demás hiperparámetros se mantienen por defecto.
- Para más información acerca de los hiperparámetros que permite ajustar
parsnip, consultar este enlace.
Flujos de trabajo (pipelines)
Los flujos de trabajo son una manera flexible de trabajar con tidymodels. Se fundamenta en la misma idea de los pipelines de scikit-learn de Python. Es posible construir nuestro flujo de trabajo con recetas y modelos declarados previamente.
Consultar más información de la biblioteca workflows.
Flujo de trabajo sin imputación:
- Flujo de trabajo con imputación:
Grid
- En este caso se utiliza la cuadrícula a través de diseños de llenado de espacio (space-filling designs), los cuales intentan encontrar una configuración de puntos (combinaciones) que cubren el espacio de parámetros con menor probabilidad de valores que se traslapan. Para este ejemplo el tamaño de la cuadrícula fue de 10.
- Para este caso particular se usan diseños de máxima entropía, descritos en el año 1987 por Shewry y Wynn en el artículo “Maximum Entropy Sampling”. También podrían ser implementados diseños de hipercubos latinos o diseños de proyección máxima. Si no se desea utilizar alguno de estos métodos, podría ser implementada una cuadrícula regular a través de métodos aleatorios (grid random).
- Mayor información en la página web de la biblioteca dials.
- A continuación se muestra la cuadrícula de búsqueda de los mejores hiperparámetros. Se evidencia que los puntos no se solapan, de tal manera que el espacio de búsqueda no es redundante.
Código
grid_xgb %>%
ggplot(aes(x = .panel_x, y = .panel_y)) +
facet_matrix(vars(mtry, min_n, tree_depth), layer.diag = 2) +
geom_point()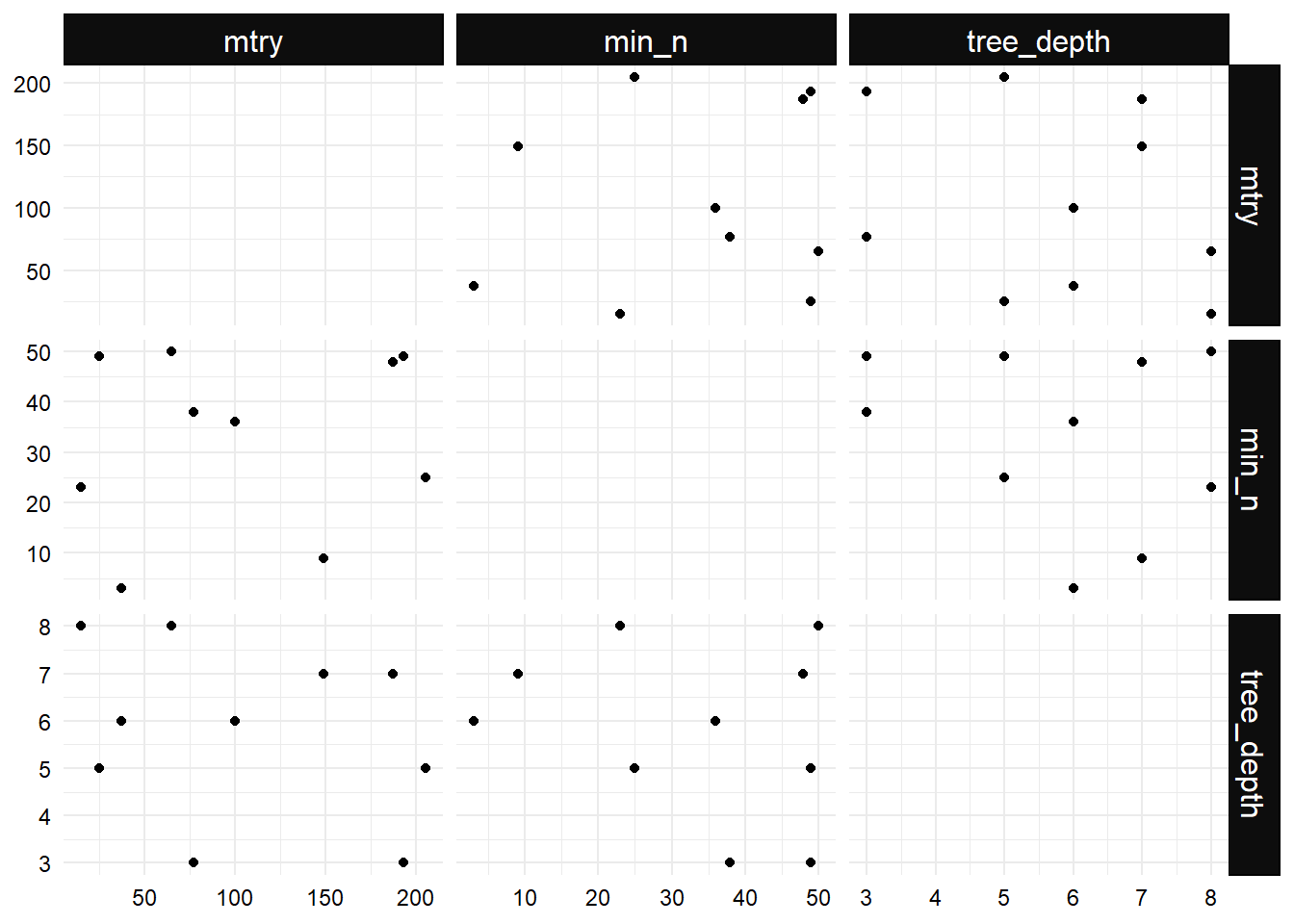
Tuning con tidymodels
- La función
tune_grid()de la biblioteca tune permite evaluar los modelos con cada combinación de paramétros establecidos previamente en la cuadrícula. - Tuning sin imputación:
Código
registerDoParallel(parallel::detectCores() - 1) # Inicio Paralelización
set.seed(2021)
tuned_no_impute <- tune_grid(
object = wf_no_impute,
resamples = config_cv,
grid = grid_xgb
)
stopImplicitCluster() # Fin Paralelización- Tuning con imputación:
Código
registerDoParallel(parallel::detectCores() - 1) # Inicio Paralelización
set.seed(2021)
tuned_si_impute <- tune_grid(
object = wf_si_impute,
resamples = config_cv,
grid = grid_xgb
)
stopImplicitCluster() # Fin ParalelizaciónResultados Accuracy
- Resultados de Accuracy en modelos sin imputación. La precisión más alta se consigue con aproximadamente 150 variables (
mtry), menos de 10 observaciones para que se produzca la división del árbol (min_n) y profunidad de más o menos 6 (tree_depth).
Código
tuned_no_impute %>%
collect_metrics() %>%
filter(.metric == "accuracy") %>%
ggplot(aes(x = mtry, y = min_n, size = tree_depth, color = mean)) +
geom_point() +
scale_color_viridis_c() +
labs(color = "Accuracy")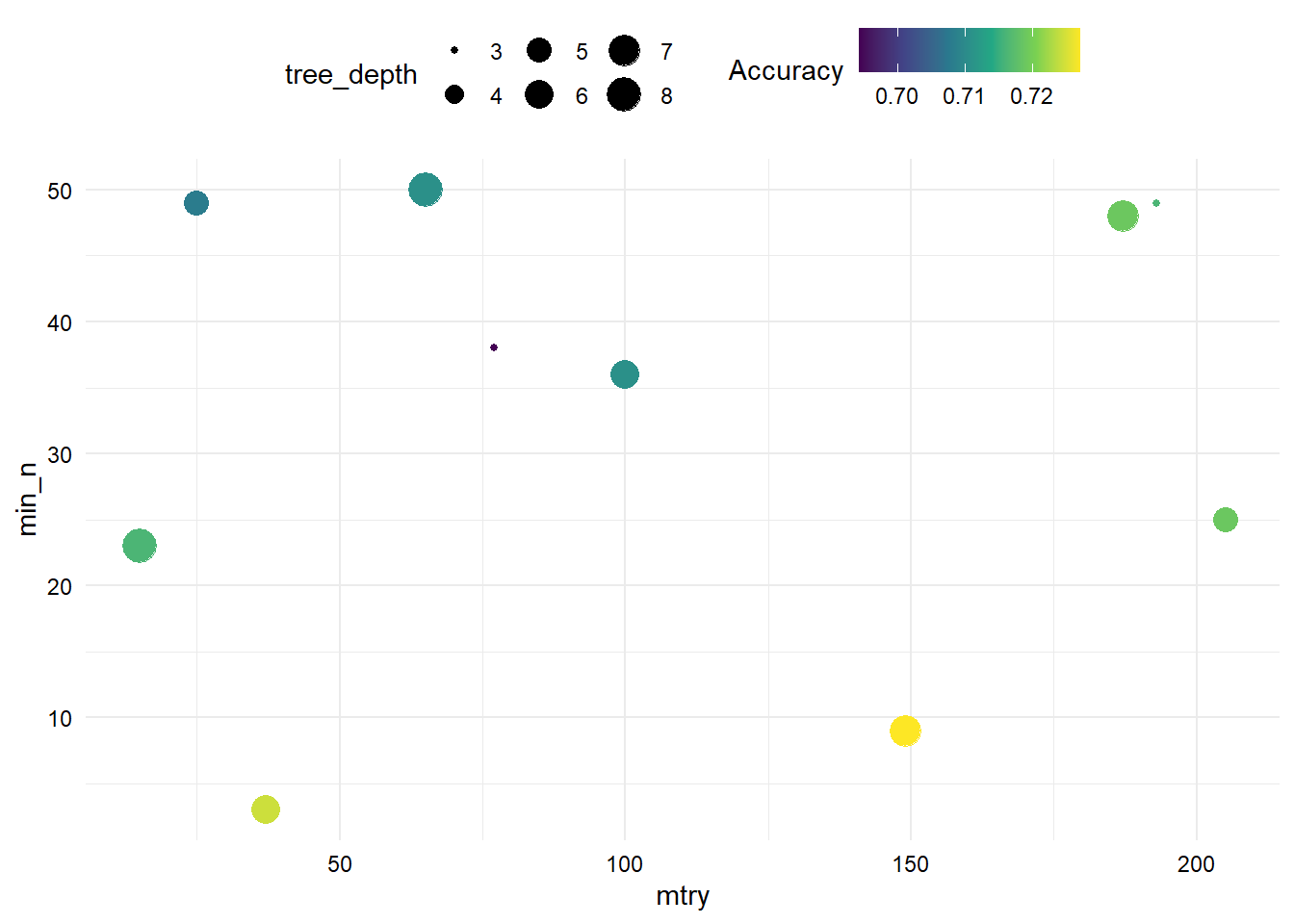
- Resultados de Accuracy en modelos con imputación. La precisión más alta se consigue con aproximadamente 25 variables (
mtry), poco menos de 50 observaciones para que se produzca la división del árbol (min_n) y profunidad de más o menos 4 (tree_depth).
Código
tuned_si_impute %>%
collect_metrics() %>%
filter(.metric == "accuracy") %>%
ggplot(aes(x = mtry, y = min_n, size = tree_depth, color = mean)) +
geom_point() +
scale_color_viridis_c() +
labs(color = "Accuracy")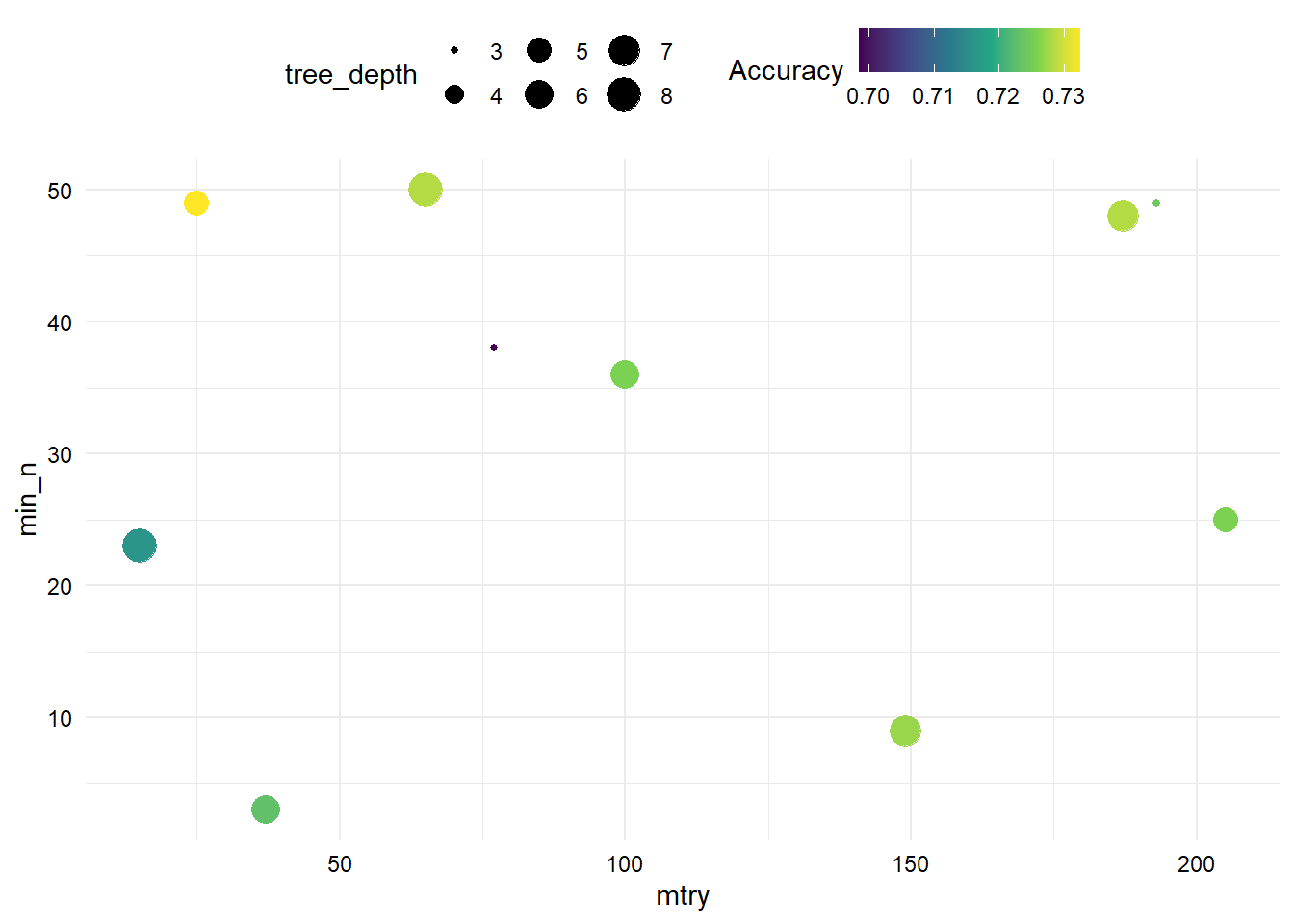
- Se observa que los mejores hiperparámetros para los algoritmos entrenados con y sin imputación, discrepan considerablemente. Aunque en este caso realicé la evaluación del desempeño de los modelos basado en la métrica Accuracy, es posible utilizar cualquier otra para problemas de clasificación.
Mejores hiperparámetros
- Mejores hiperparámetros en modelos sin imputación:
Código
mejor_no_impute <- tuned_no_impute %>%
select_best(metric = "accuracy")
mejor_no_impute- Mejores hiperparámetros en modelos con imputación:
Código
mejor_si_impute <- tuned_si_impute %>%
select_best(metric = "accuracy")
mejor_si_imputeAjuste final
- Modelo sin imputación:
Código
final_no_impute <- finalize_workflow(
x = wf_no_impute,
parameters = mejor_no_impute
) %>%
fit(data = train)- Modelo con imputación:
Código
final_si_impute <- finalize_workflow(
x = wf_si_impute,
parameters = mejor_si_impute
) %>%
fit(data = train)Predicciones Train
- Modelo sin imputación:
- Modelo con imputación:
Predicciones Test
- Modelo sin imputación:
- Modelo con imputación:
Matriz de confusión Train
- Matriz de confusión modelo sin imputación:
Código
data.frame(
predicho = as.factor(pred_no_impute_train$.pred_class),
real = as.factor(train$diagnosis)
) %>%
conf_mat(truth = real, estimate = predicho) %>%
pluck(1) %>%
as_tibble() %>%
ggplot(aes(x = Prediction, y = Truth, alpha = n)) +
geom_tile(show.legend = FALSE) +
geom_text(aes(label = n), colour = "white", alpha = 1, size = 8)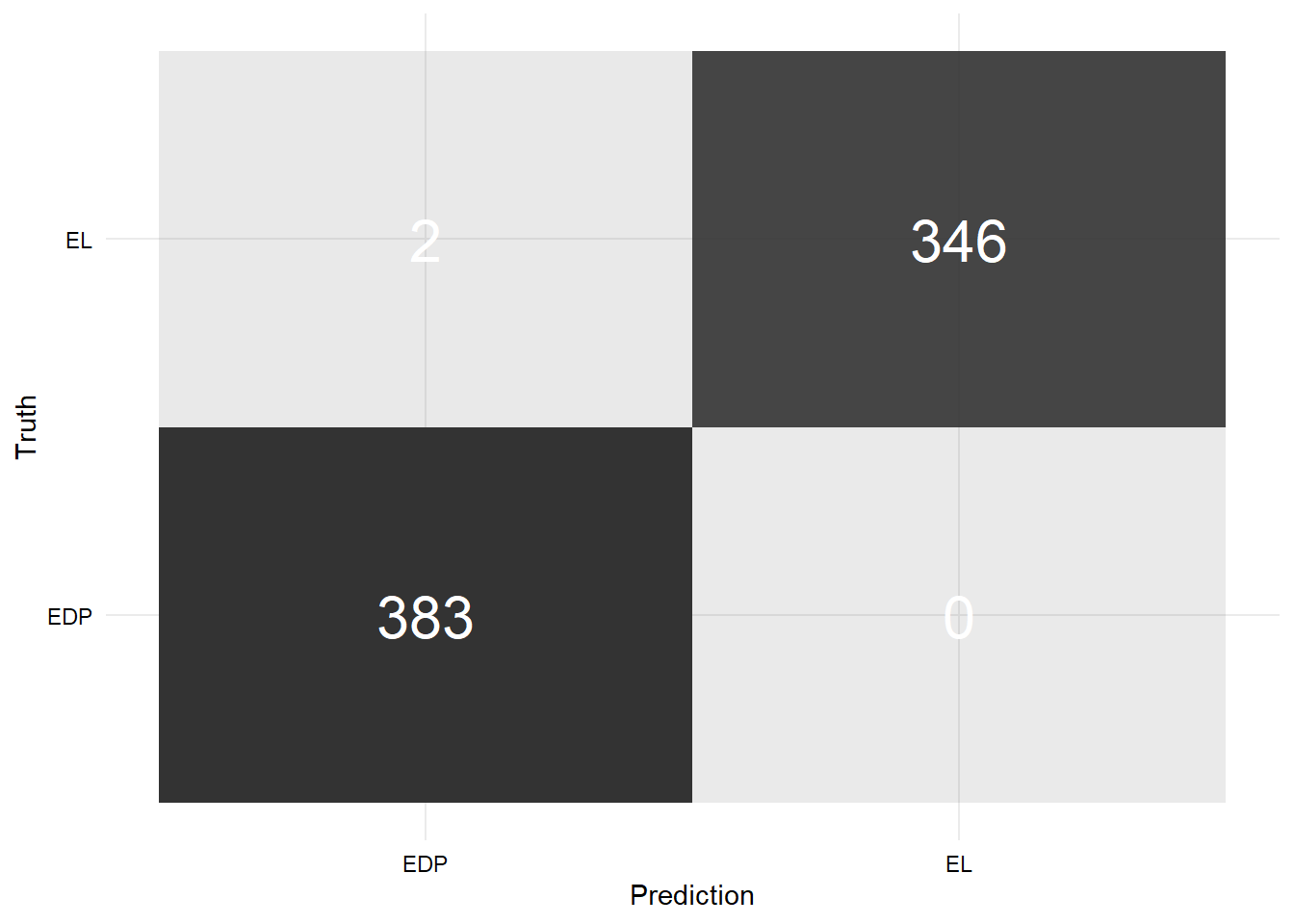
- Matriz de confusión modelo con imputación:
Código
data.frame(
predicho = as.factor(pred_si_impute_train$.pred_class),
real = as.factor(train$diagnosis)
) %>%
conf_mat(truth = real, estimate = predicho) %>%
pluck(1) %>%
as_tibble() %>%
ggplot(aes(x = Prediction, y = Truth, alpha = n)) +
geom_tile(show.legend = FALSE) +
geom_text(aes(label = n), colour = "white", alpha = 1, size = 8)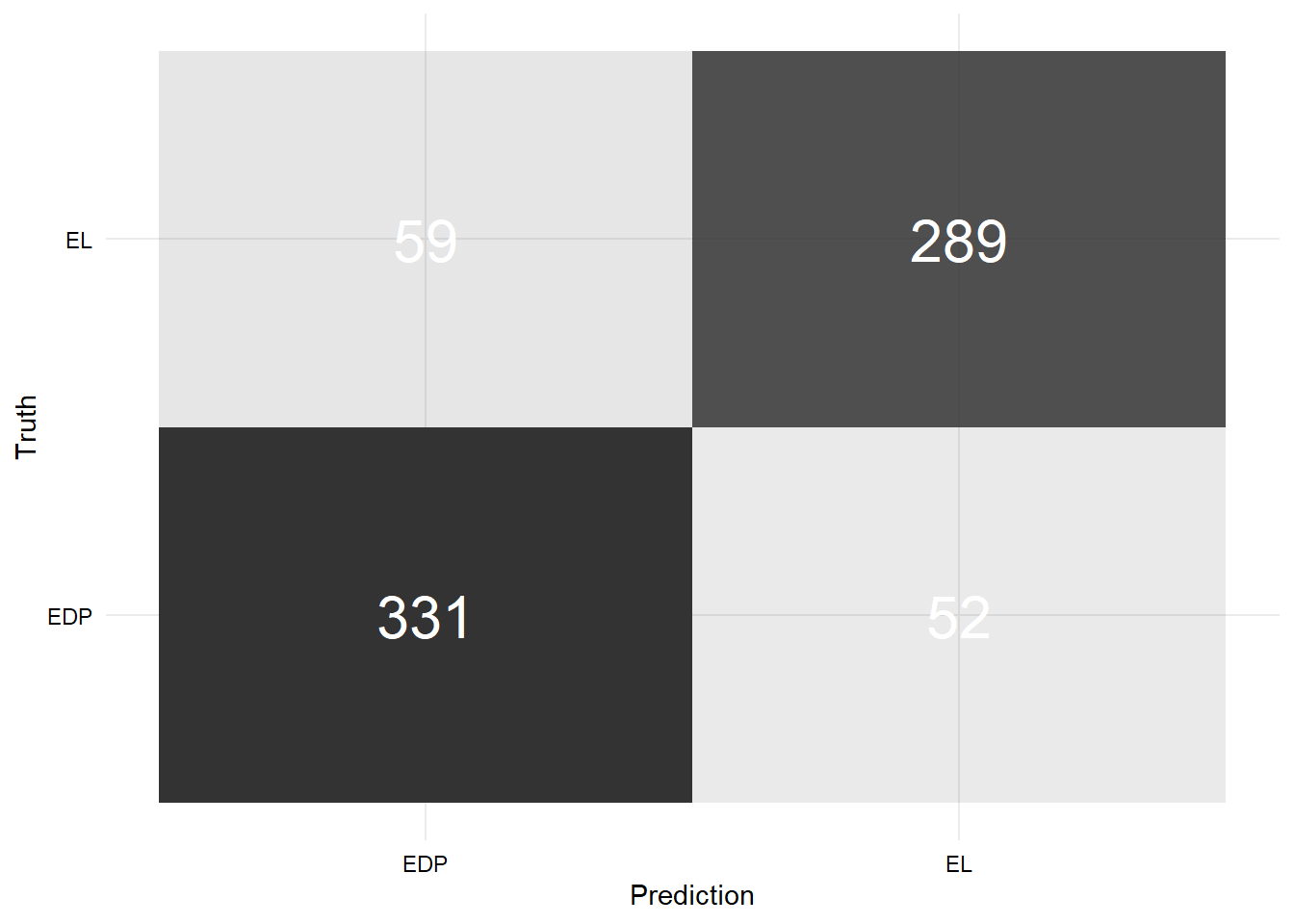
Matriz de confusión Test
- Matriz de confusión modelo sin imputación:
Código
data.frame(
predicho = as.factor(pred_no_impute_test$.pred_class),
real = as.factor(test$diagnosis)
) %>%
conf_mat(truth = real, estimate = predicho) %>%
pluck(1) %>%
as_tibble() %>%
ggplot(aes(x = Prediction, y = Truth, alpha = n)) +
geom_tile(show.legend = FALSE) +
geom_text(aes(label = n), colour = "white", alpha = 1, size = 8)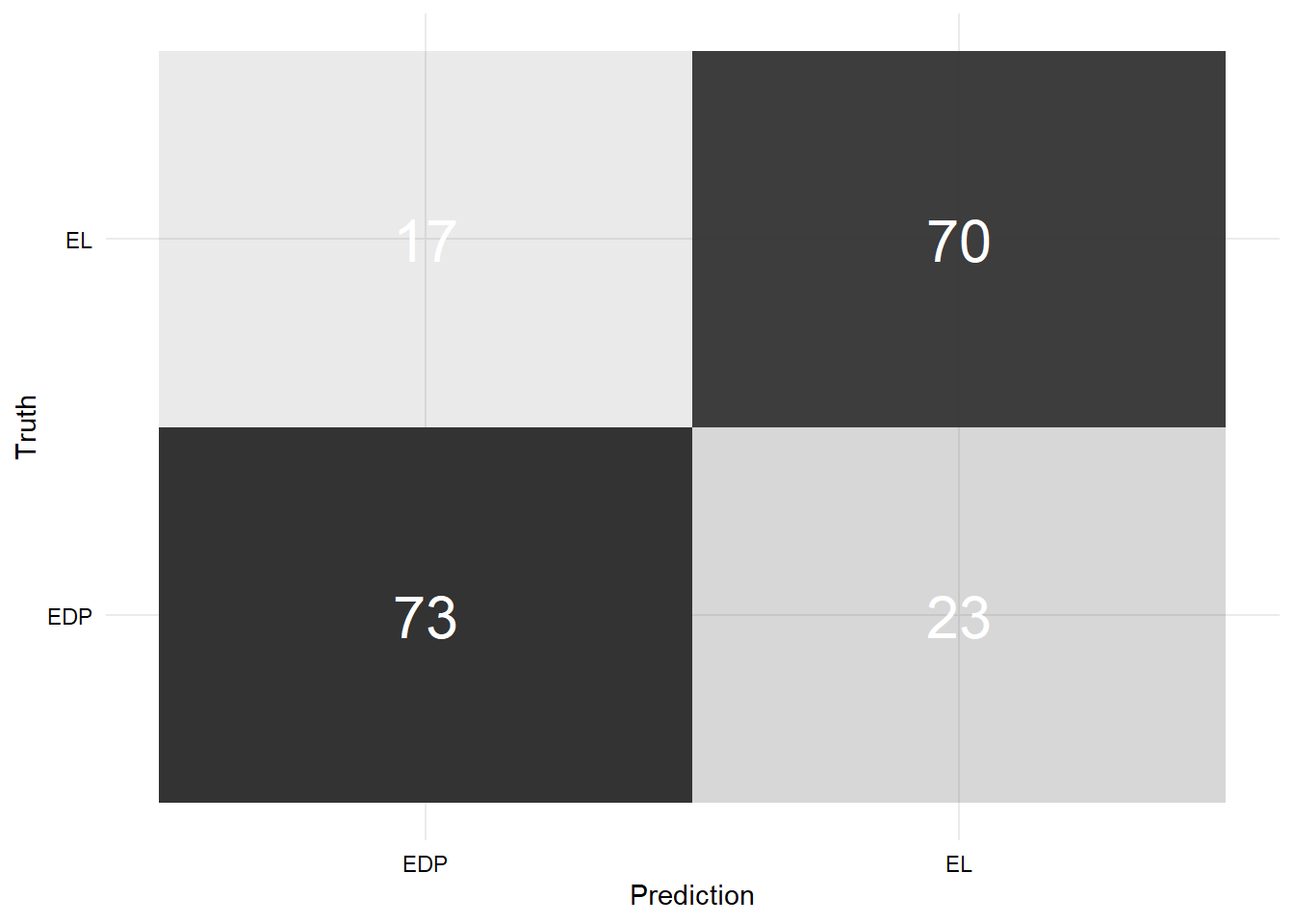
- Matriz de confusión modelo con imputación:
Código
data.frame(
predicho = as.factor(pred_si_impute_test$.pred_class),
real = as.factor(test$diagnosis)
) %>%
conf_mat(truth = real, estimate = predicho) %>%
pluck(1) %>%
as_tibble() %>%
ggplot(aes(x = Prediction, y = Truth, alpha = n)) +
geom_tile(show.legend = FALSE) +
geom_text(aes(label = n), colour = "white", alpha = 1, size = 8)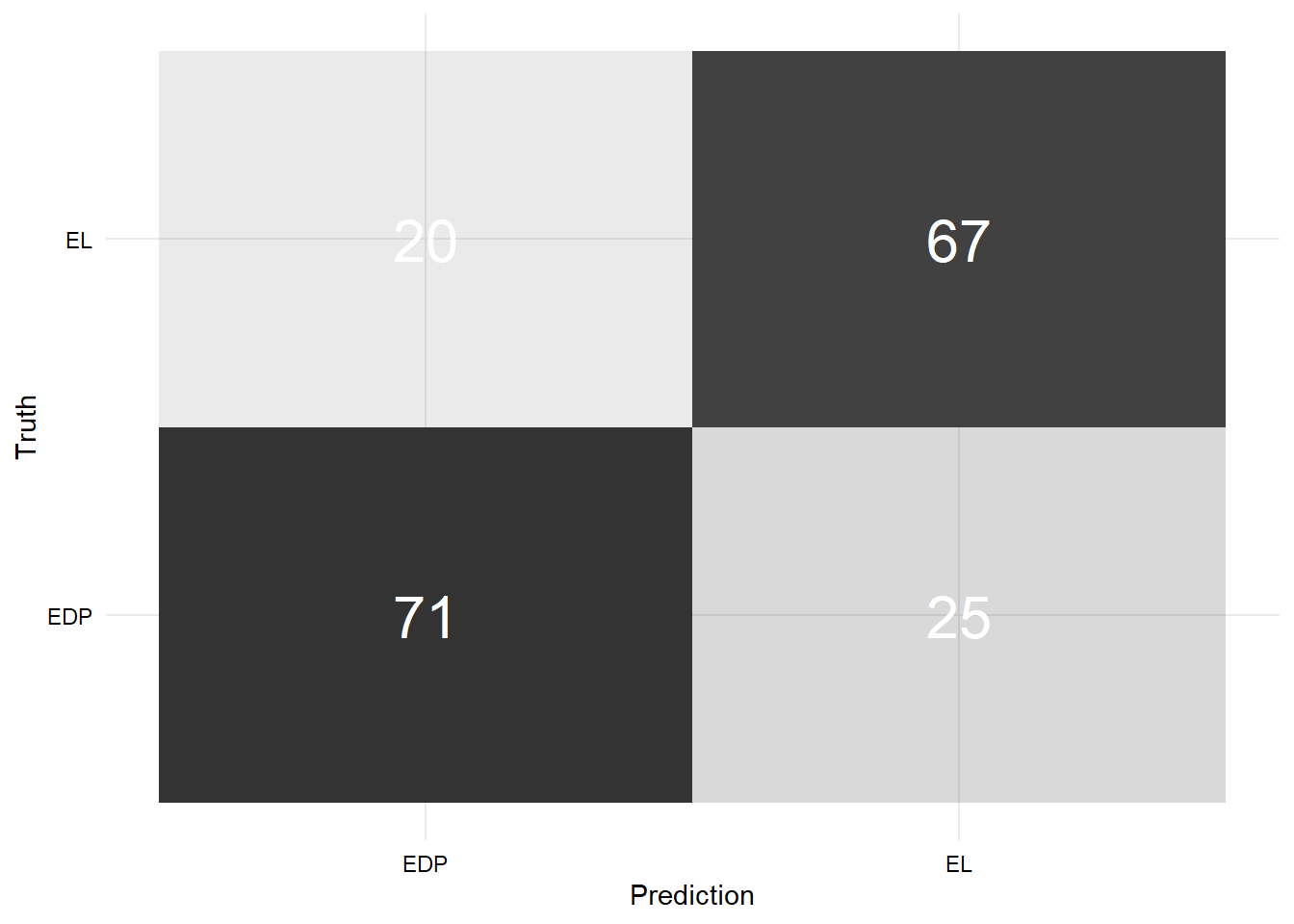
Desempeño de modelos
- Genero una base de datos con los resultados de las clases predichas en cada tipo de modelo (con y sin imputación) para los conjuntos de entrenamiento y prueba.
Código
tabla_accuracy <- data.frame(
predicho = pred_no_impute_train$.pred_class,
real = train$diagnosis,
datos = "Train",
tipo = "Sin imputación"
) %>%
bind_rows(
data.frame(
predicho = pred_si_impute_train$.pred_class,
real = train$diagnosis,
datos = "Train",
tipo = "Con imputación"
)
) %>%
bind_rows(
data.frame(
predicho = pred_no_impute_test$.pred_class,
real = test$diagnosis,
datos = "Test",
tipo = "Sin imputación"
)
) %>%
bind_rows(
data.frame(
predicho = pred_si_impute_test$.pred_class,
real = test$diagnosis,
datos = "Test",
tipo = "Con imputación"
)
) %>%
mutate(across(where(is.character), as.factor))
tabla_accuracy %>%
group_by(datos, tipo) %>%
summarise(accuracy = accuracy_vec(truth = real, estimate = predicho)) %>%
kable(caption = "Accuracy en train y test para dos modelos XGBoost")| datos | tipo | accuracy |
|---|---|---|
| Test | Con imputación | 0.7540984 |
| Test | Sin imputación | 0.7814208 |
| Train | Con imputación | 0.8481532 |
| Train | Sin imputación | 0.9972640 |
- Gráfico Accuracy: la capacidad predictiva es superior en el modelo que fue entrenado sin acudir a la imputación de datos.
Código
tabla_accuracy %>%
group_by(datos, tipo) %>%
summarise(accuracy = accuracy_vec(truth = real, estimate = predicho)) %>%
ggplot(aes(x = tipo, y = accuracy, color = datos, fill = datos)) +
geom_col(position = "dodge", alpha = 0.8) +
scale_color_jama() +
scale_fill_jama() +
labs(x = "Preprocesamiento", y = "Accuracy",
color = "", fill = "")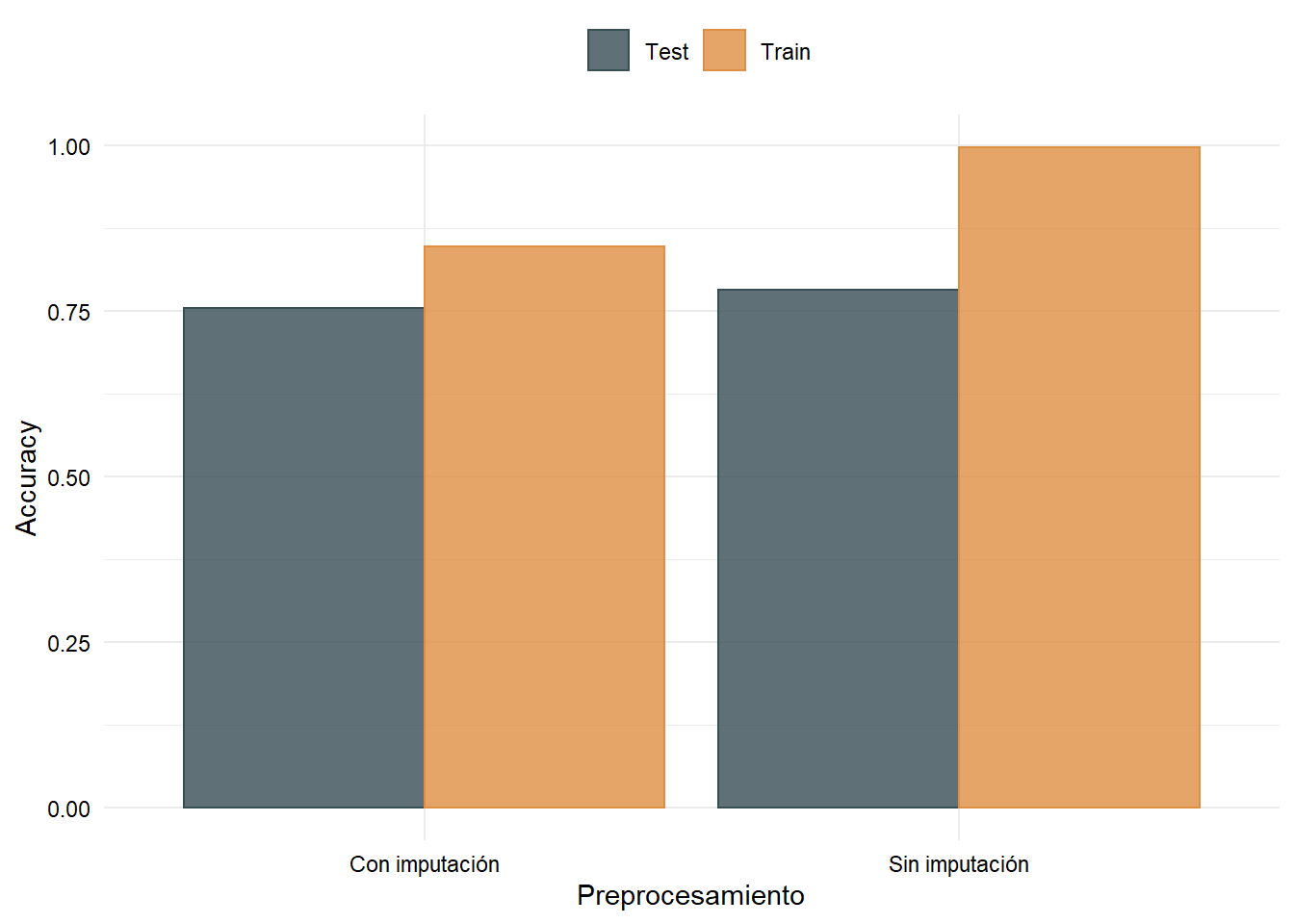
Importancia de variables
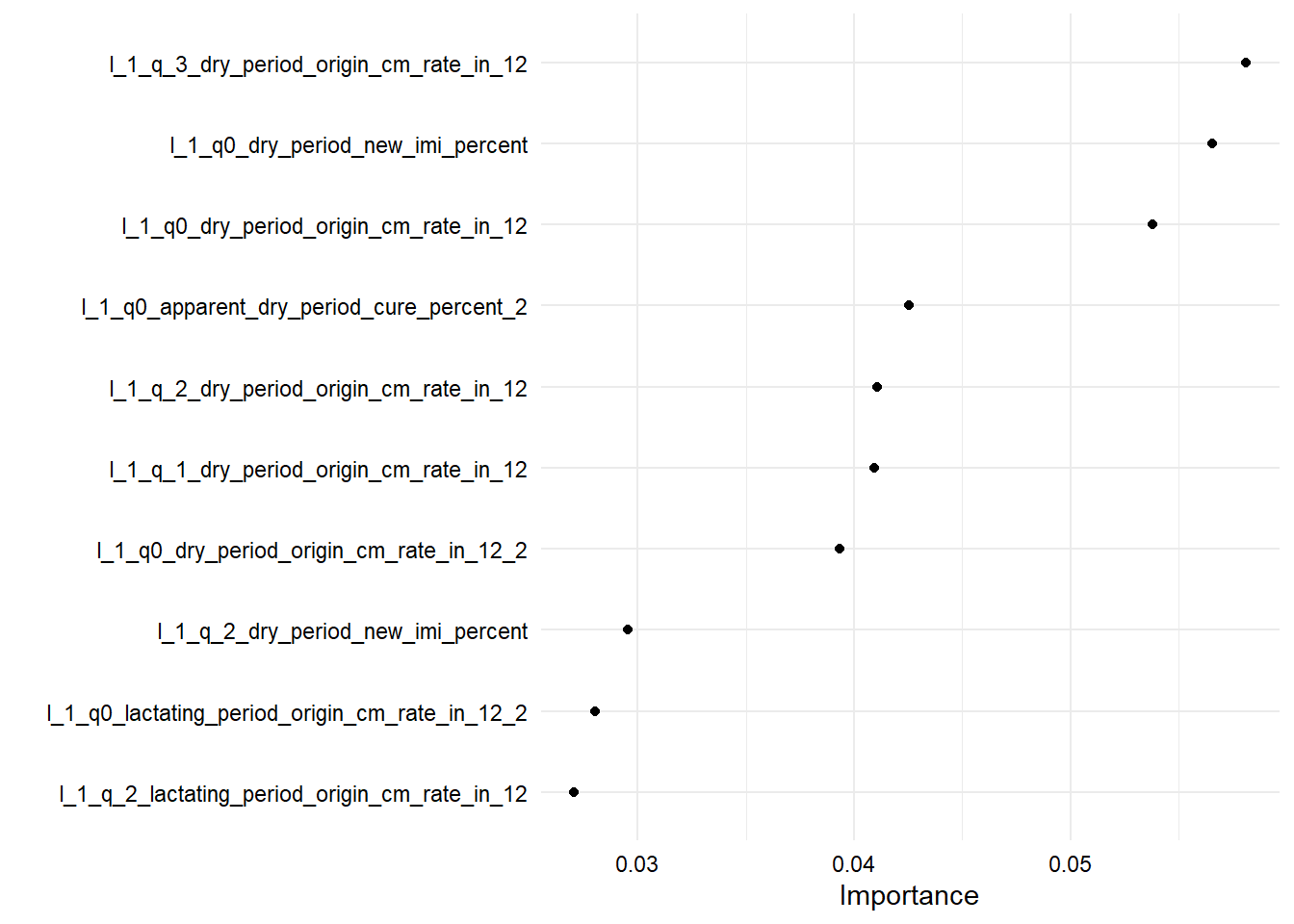
- 10 variables de mayor importancia en modelo sin imputación:
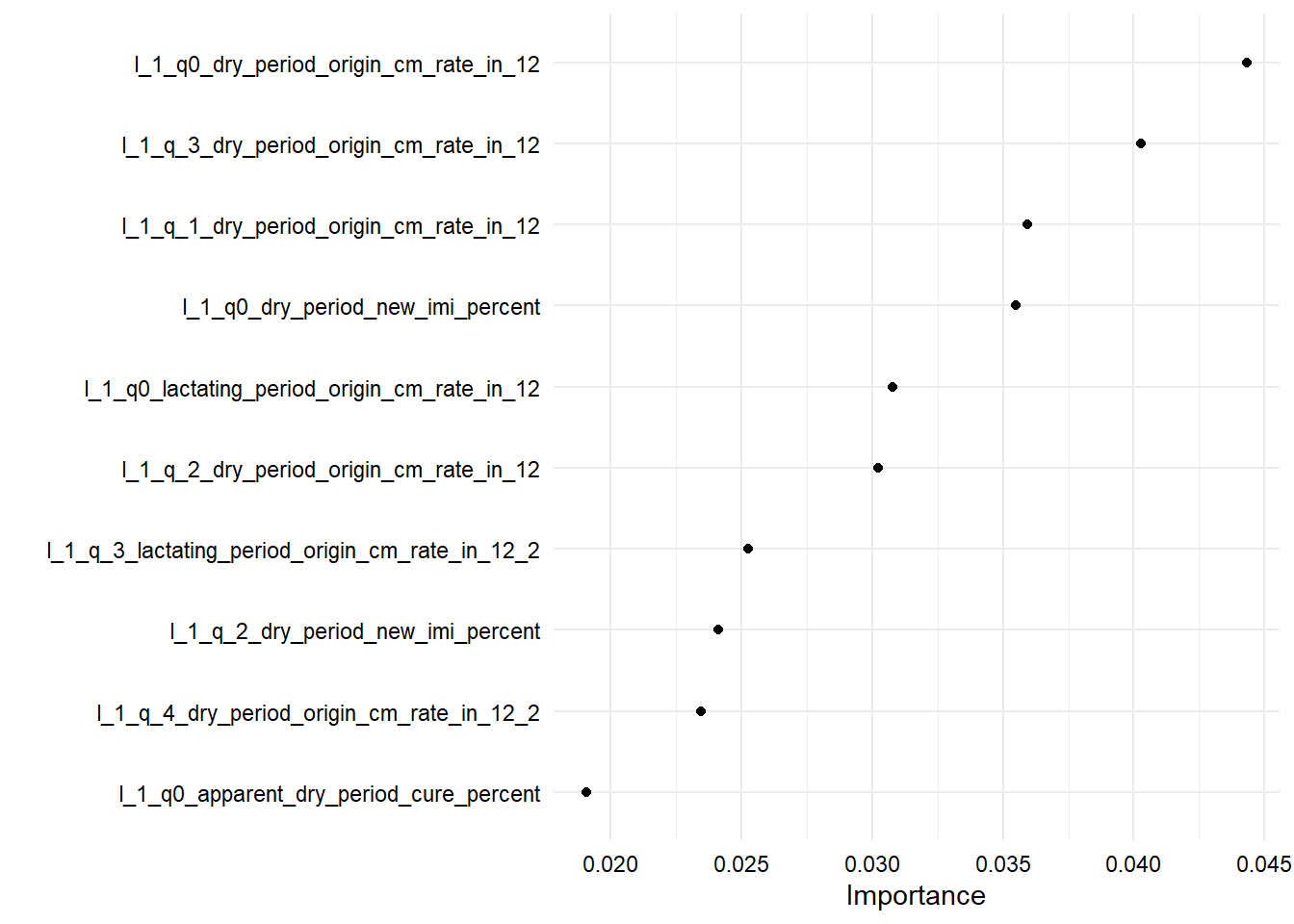
- 10 variables de mayor importancia en modelo sin imputación:
Referencias
- Hyde, R.M., Down, P.M., Bradley, A.J. et al. “Automated prediction of mastitis infection patterns in dairy herds using machine learning”. Sci Rep 10, 4289 (2020). https://doi.org/10.1038/s41598-020-61126-8
- Chen Tianqi, Guestrin Carlos. “XGBoost: A Scalable Tree Boosting System”. CoRR, Vol 1603.02754 (2016). https://arxiv.org/abs/1603.02754
- Boehmke Bradley, Greenwell Brandon. “Hands-On Machine Learning with R”. Chapman and Hall/CRC (2019). https://bradleyboehmke.github.io/HOML/gbm.html
- Shewry, M, and H Wynn. “Maximum Entropy Sampling.” Journal of Applied Statistics 14 (2): 165–70 (1987). https://doi.org/10.1080/02664768700000020
- Kuhn Max, Silge Julia. “Tidy Modeling with R”. (2020). https://www.tmwr.org/