Motivación
Configuración
Ecuación diferencial logística
Expresión matemática
\[\frac{\partial x}{\partial t} = \alpha x_t \times (1 - x_t)\]
Parametrización en R
Función 1
- Se construyen dos funciones para realizar las simulaciones:
growth()eiterGrowth() - Se definen los siguientes parámetros para la función
growth():-
rate(\(\alpha\)): tasa de crecimento o razón de cambio. Relación de la natalidad con la mortalidad. -
xt: tamaño de la población inicial (%). \(0 \leq x_t \leq 1\) - Retorno: esta función devuelve el cálculo de la población mediante la ecuación anterior.
-
- Se definen los siguientes parámetros para la función
iterGrowth():-
rate(\(\alpha\)): tasa de crecimento o razón de cambio. Relación de la natalidad con la mortalidad -
xt: tamaño de la población inicial (%). \(0 \leq x_t \leq 1\) -
t: número de generaciones (tiempo generacional) para evaluar el crecimiento poblacional. -
xinit: es la mismaxt, es decir, la población inicial. Aunque se repite es útil para registrar el tamaño inicial de la población, ya quextcambia al realizar la iteración recursiva conwhile(). -
Retorno: esta función devuelve el cálculo de la población hasta el tiempo
t, haciendo uso de la funcióngrowth()y sus parámetros específicos.
-
Código
# =========== Función para simulación con ecuación logística
# Crecimiento = (rate * xt) * (1 - xt)
growth <- function(rate, xt) {
pob = (rate * xt) * (1 - xt)
return(pob)
}
# Función recursiva para obtener la población para cada tiempo "t"
iterGrowth <- function(xt, rate, t, xinit) {
res = NULL
if (t == 0) {
res = xt
return(res)
} else if (t == 1) {
res = growth(rate = rate, xt = xt)
return(res)
} else{
i = 1
while (i <= (t)) {
res[i + 1] = growth(rate = rate, xt = xt)
xt = growth(rate = rate, xt = xt)
i = i + 1
}
res[1] = xinit
return(res)
}
}Función 2
- Esta función facilita el proceso de conformar un
tibblecon los resultados de la simulación.
Simulaciones
Simulación 1
- ¿Qué pasa en 100 generaciones con una población cuya natalidad es 1.72 veces mayor que la mortalidad y su población actual es 62% del máximo teórico? ¿En qué valor se estabiliza el crecimiento de la población? ¿Se extingue la población?
-
rate: 1.72 -
xt: 0.62 -
t: 100 -
xinit: 0.62
-
Código
r <- 1.72
xt <- 0.62
t <- 100
xinit <- xt
iterGrowth(rate = r, xt = xt, t = t, xinit = xinit) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
ggplot(aes(x = t, y = pob)) +
geom_line(color = "firebrick2") +
labs(x = "Tasa",
y = "Estabilidad poblacional",
title = "Equilibrio poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'))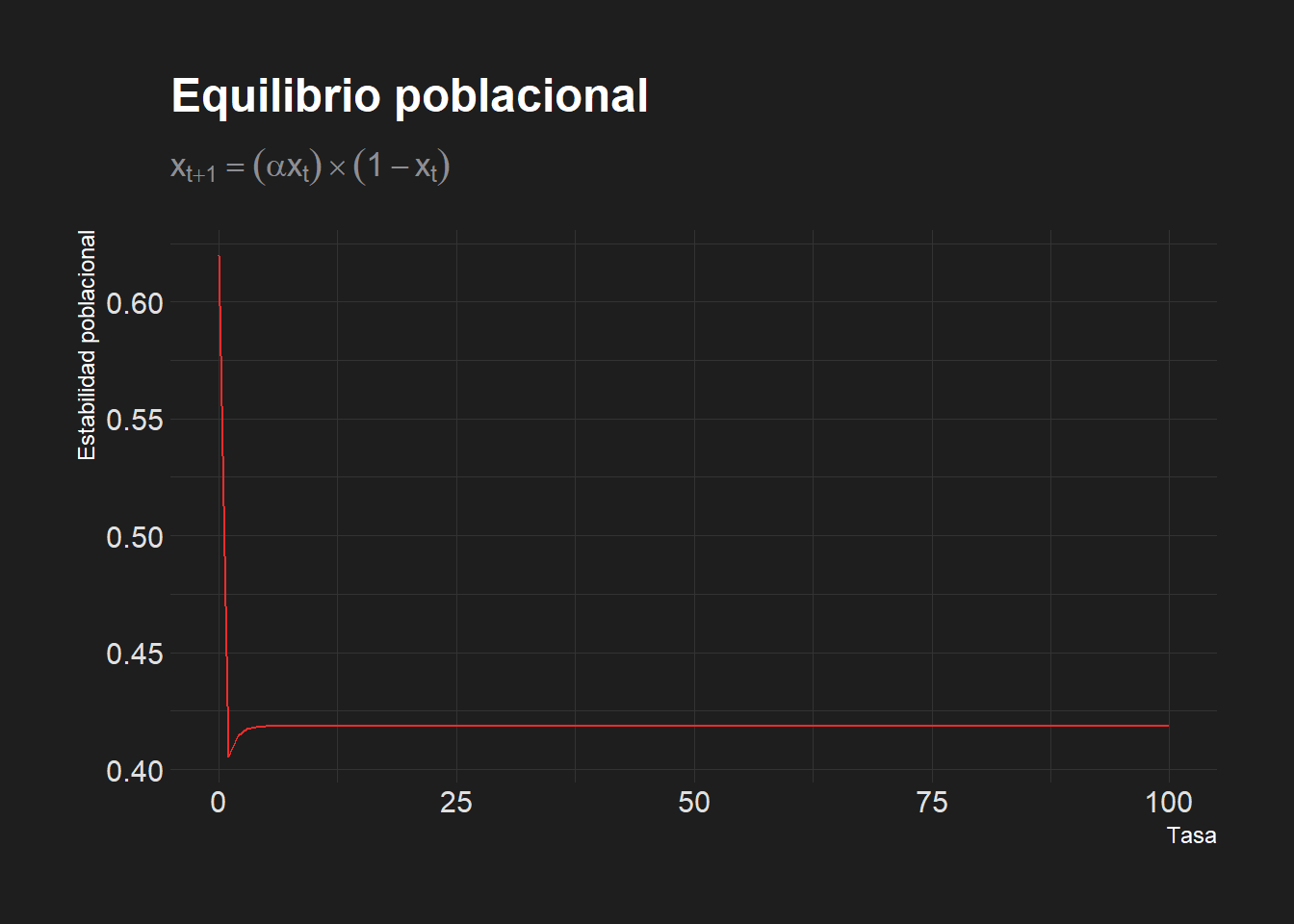
Simulación 2
- ¿Qué pasa en 100 generaciones con una población cuya natalidad es 0.72 veces menor que la mortalidad y su población actual es 62% del máximo teórico? ¿En qué valor se estabiliza el crecimiento de la población? ¿Se extingue la población?
-
rate: 0.72 -
xt: 0.62 -
t: 100 -
xinit: 0.62
-
Código
r <- 0.72
xt <- 0.62
t <- 100
xinit <- xt
iterGrowth(rate = r, xt = xt, t = t, xinit = xinit) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
ggplot(aes(x = t, y = pob)) +
geom_line(color = "firebrick2") +
labs(x = "Tasa",
y = "Equilibrio poblacional",
title = "Estabilidad poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'))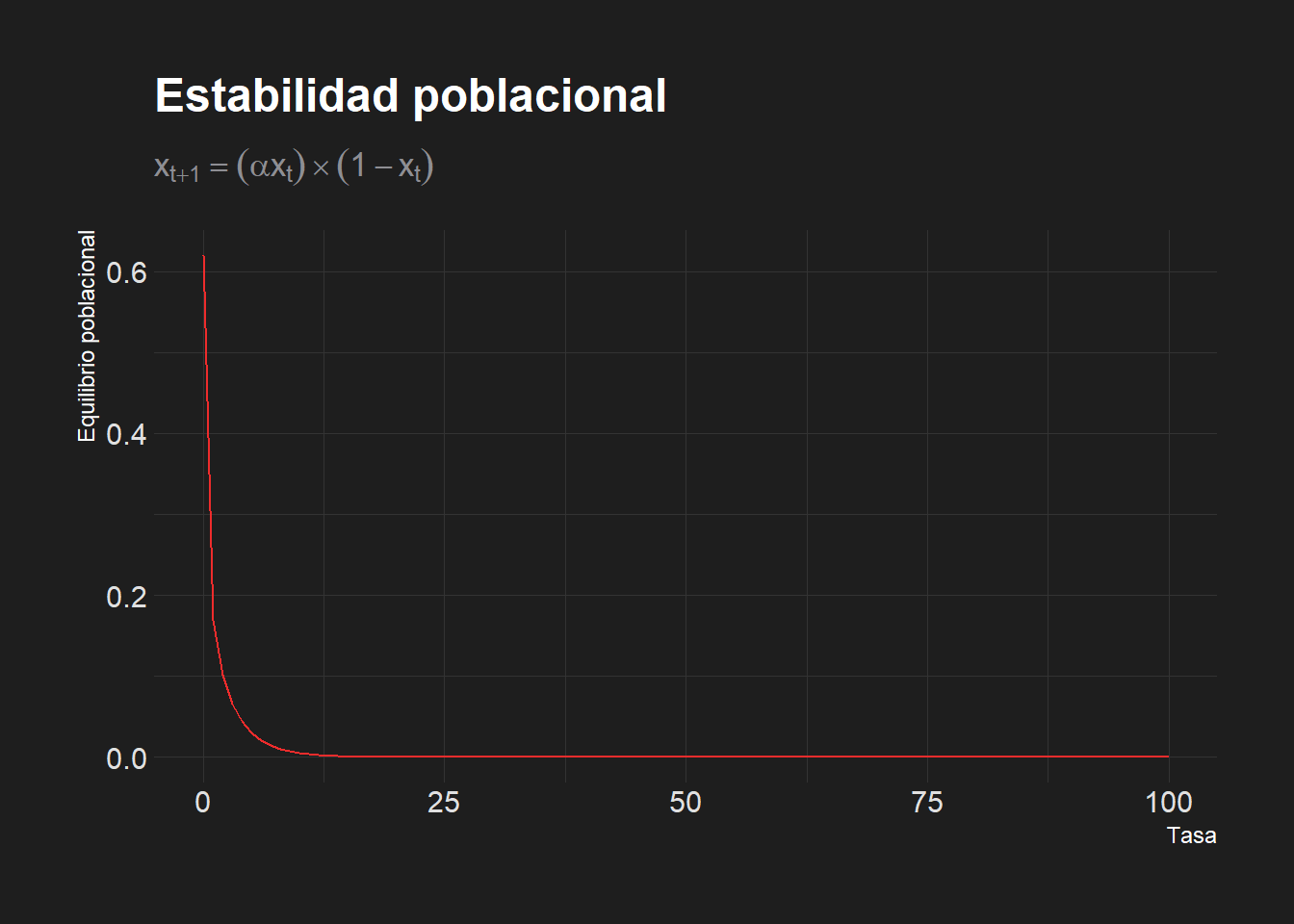
Simulación 3
- ¿Qué pasa en 100 generaciones con una población cuya natalidad es igual que la mortalidad y su población actual es 62% del máximo teórico? ¿En qué valor se estabiliza el crecimiento de la población? ¿Se extingue la población?
-
rate: 0.72 -
xt: 0.62 -
t: 100 -
xinit: 0.62
-
Código
r <- 1
xt <- 0.62
t <- 100
xinit <- xt
iterGrowth(rate = r, xt = xt, t = t, xinit = xinit) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
ggplot(aes(x = t, y = pob)) +
geom_line(color = "firebrick2") +
labs(x = "Tasa",
y = "Equilibrio poblacional",
title = "Estabilidad poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'))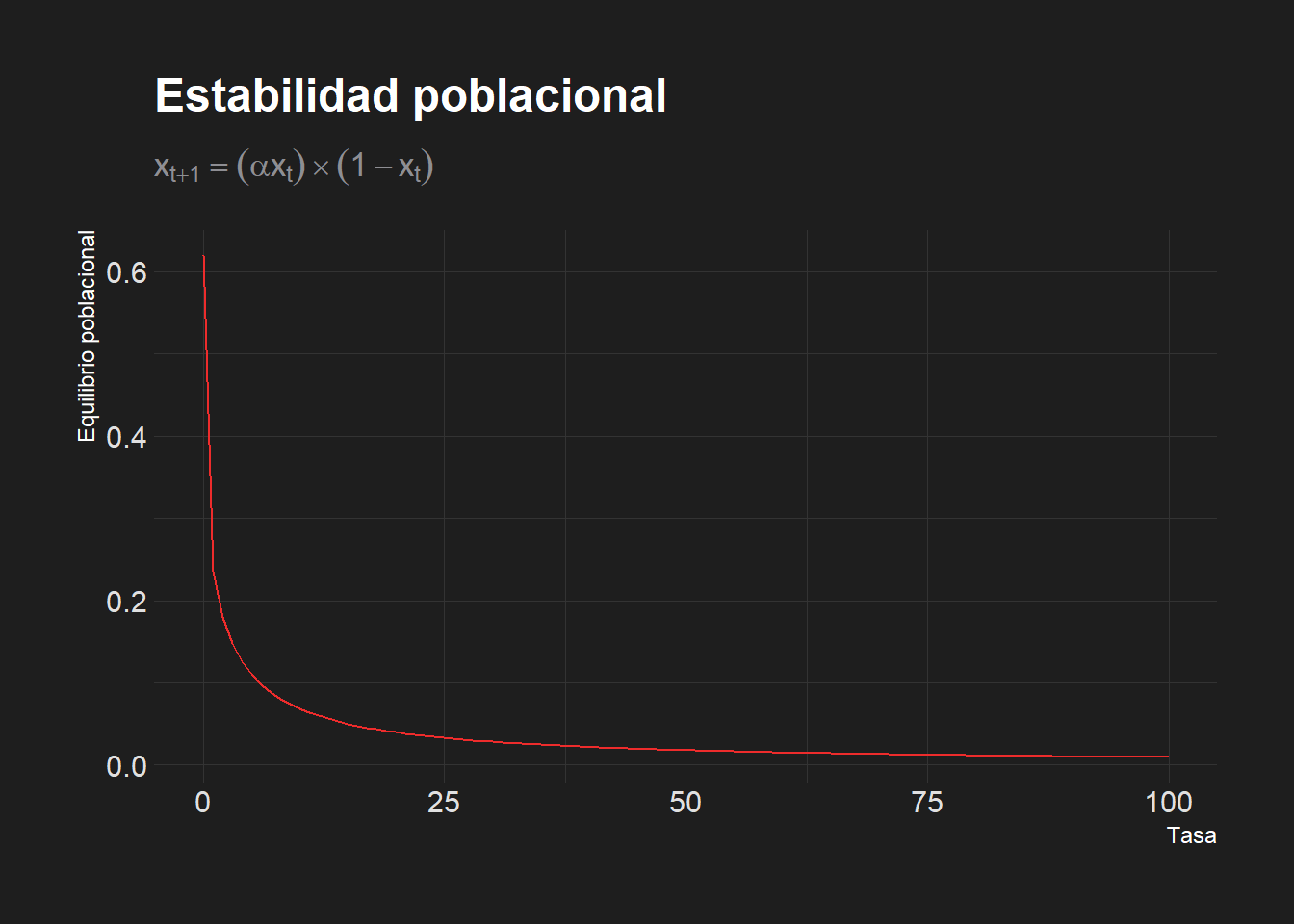
3 simulaciones en 1
- Podemos graficar las tres simulaciones anteriores en un sólo gráfico.
Código
# ============== Simulación 3 en 1
# Parámetros específico
r_sim1 <- 1.72
r_sim2 <- 0.72
r_sim3 <- 1
# Parámetros generales
xt <- 0.62
t <- 100
xinit <- xt
# Uniendo datos de simulaciones
sim_1 <-
iterGrowth(
rate = r_sim1,
xt = xt,
t = t,
xinit = xinit
) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
mutate(rate = r_sim1)
sim_2 <-
iterGrowth(
rate = r_sim2,
xt = xt,
t = t,
xinit = xinit
) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
mutate(rate = r_sim2)
sim_3 <-
iterGrowth(
rate = r_sim3,
xt = xt,
t = t,
xinit = xinit
) %>%
enframe() %>%
mutate(t = name - 1) %>%
select(t, pob = value) %>%
mutate(rate = r_sim3)
sim_total <-
bind_rows(sim_1, sim_2, sim_3)
sim_total %>%
mutate(rate = as.factor(rate)) %>%
ggplot(aes(x = t, y = pob, color = rate)) +
geom_line() +
scale_color_manual(values = c("#76b49f", "#ef3840", "#edea6f")) +
labs(x = "Tasa",
y = "Equilibrio poblacional",
title = "Estabilidad poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)')) 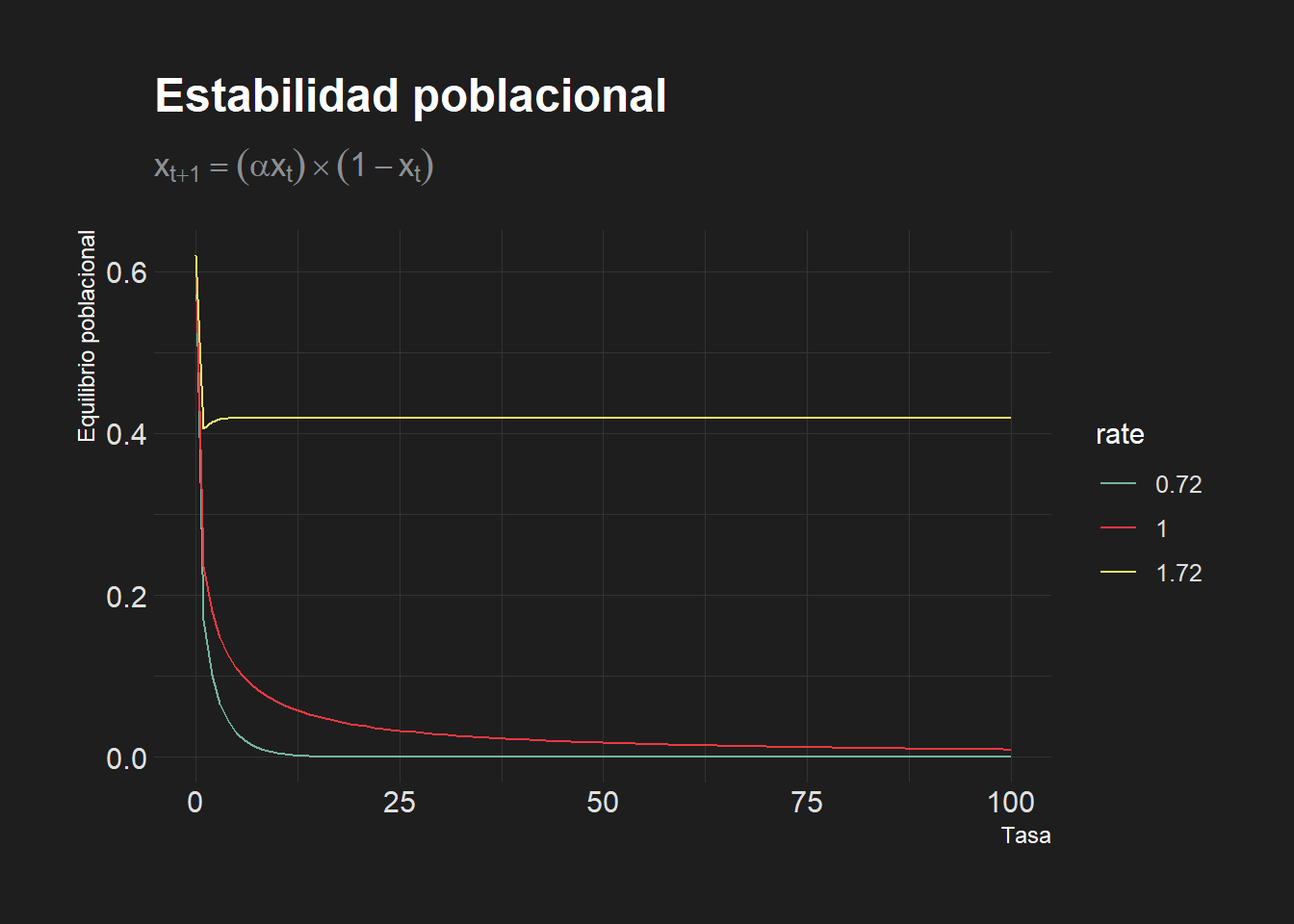
Simulación 4
- En esta simulación se implementan diferentes tasas de crecimiento para ver el resultado en el equilibrio poblacional (en 100 generaciones) con una población cuyo tamaño actual es 62% del máximo teórico.
Código
# Parámetros
r <- seq(from = 0.1, to = 3.6, by = 0.1)
xt <- 0.62
t <- 100
xinit <- xt
# Gráfico
r %>%
map_df(.x = .,
.f = ~ dfGrowth(
rate = .,
xt = xt,
t = t,
xinit = xinit
)) %>%
ggplot(aes(x = t, y = pob, color = rate)) +
geom_line(alpha = 0.2) +
scale_color_viridis_d() +
labs(x = "Tasa",
y = "Equilibrio poblacional",
title = "Estabilidad poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'))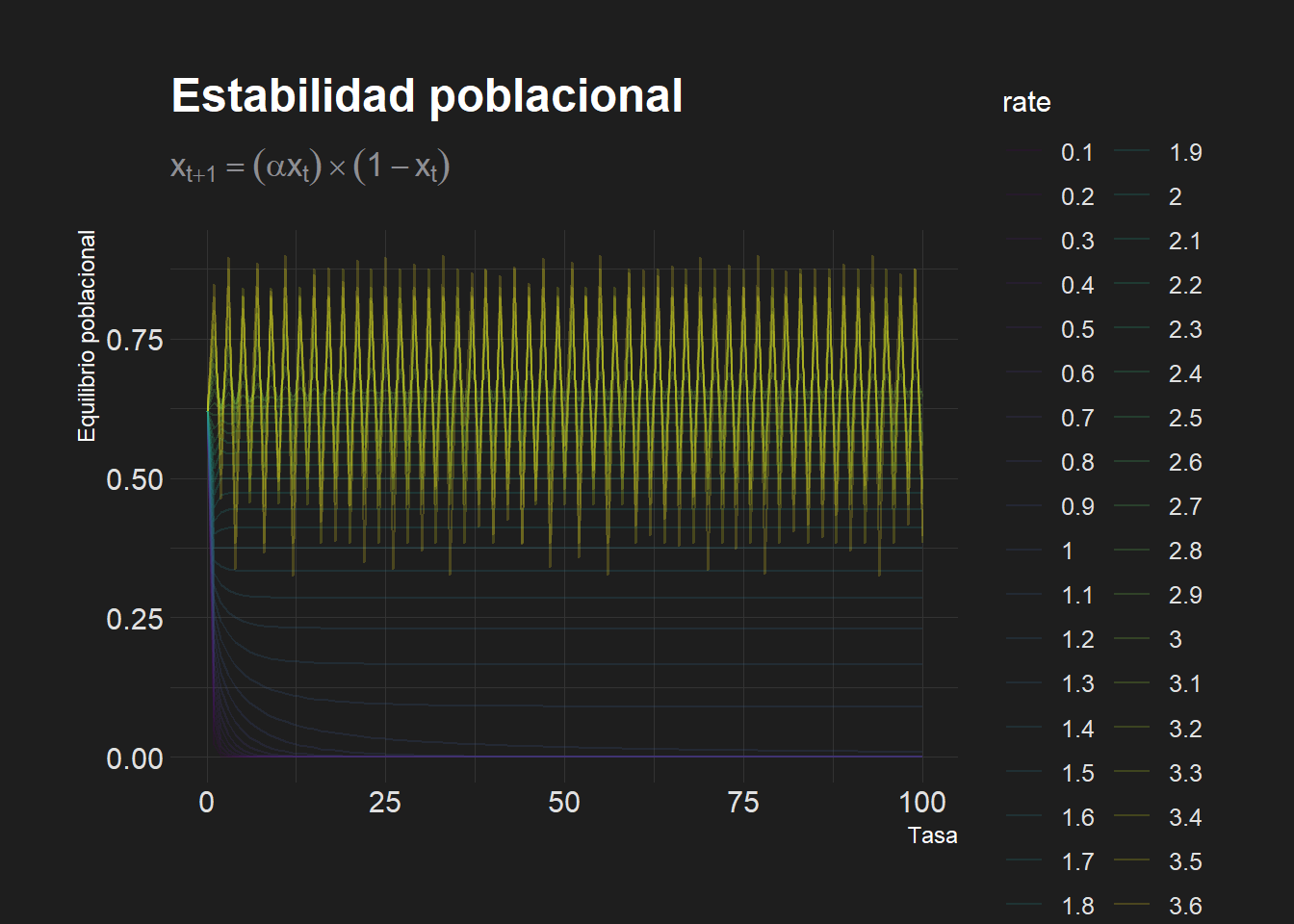
Simulación 5
- En esta simulación tomo tasas de crecimiento entre 3.5 y 3.8 (justamente donde aparece el caos) para ver el resultado en el equilibrio poblacional (en 100 generaciones) con una población cuyo tamaño actual es 62% del máximo teórico. Nota: para facilitar la visualización de los patrones 😎 se presenta de forma interactiva con
plotly.
Código
# Parámetros
r <- seq(from = 3.5, to = 3.8, length = 20)
xt <- 0.62
t <- 100
xinit <- xt
# Gráfico
ggplotly(
r %>%
map_df(.x = .,
.f = ~ dfGrowth(
rate = .,
xt = xt,
t = t,
xinit = xinit
)) %>%
ggplot(aes(x = t, y = pob, color = rate)) +
geom_line(alpha = 0.2) +
scale_color_viridis_d() +
labs(x = "Tasa",
y = "Equilibrio poblacional",
title = "Estabilidad poblacional",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'))
)Diagrama de bifurcación
Simulación completa
-
rate: 10 mil valores desde 0.1 a 3.8 -
xt: 0.62 -
t: 2 mil -
xinit: 0.62 -
Notas:
- Estoy asumiendo que la estabilidad poblacional se logra en la mitad del tiempo, que para este ejemplo corresponde a mil.
- Como la simulación se demora más de 20 mintuos decidí guardar el archivo con los resultados e importarlos para construir los diagramas de bifurcación.
Código
# Parámetros
r <- seq(from = 0, to = 4, length = 1000)
xt <- 0.62
t <- 2000
xinit <- xt
estabPob <- t / 2
# Simulación
set.seed(2022)
g <- r %>%
map2_df(
.x = .,
.y = t,
.f = ~ prueba(
rate = .,
xt = xt,
t = sample.int(n = .y, size = 1),
xinit = xinit
) %>% slice(sample.int(n = .y, size = 1))
)
# Exportando resultados simulación
write_csv(x = g, "data_simulation_rates.csv")Opción 1
Código
result_simulation <- read_csv("data/data_simulation_rates.csv")
result_simulation %>%
ggplot(aes(x = rate, y = pob)) +
geom_point(size = 0.1, color = "white")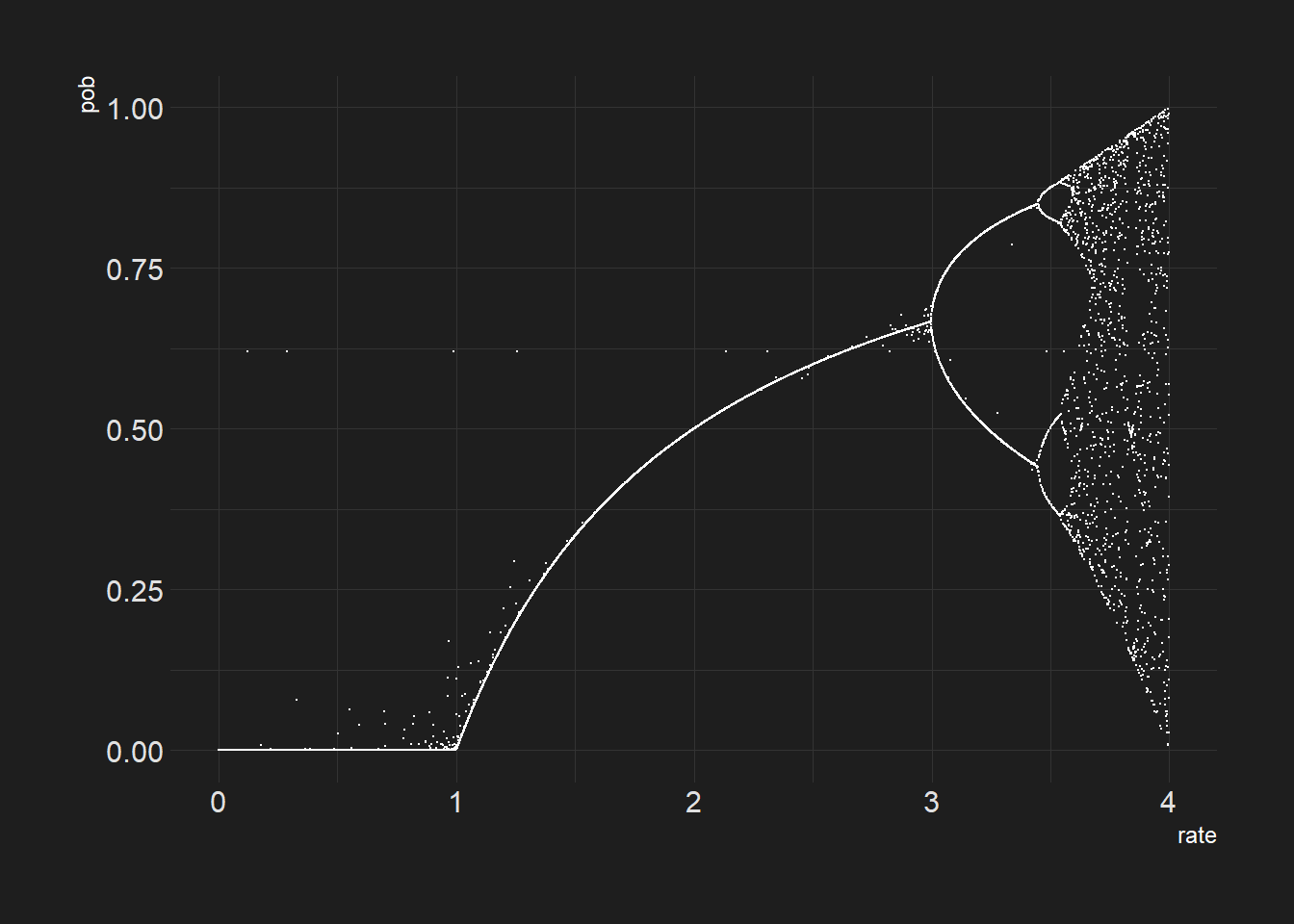
Opción 2
Código
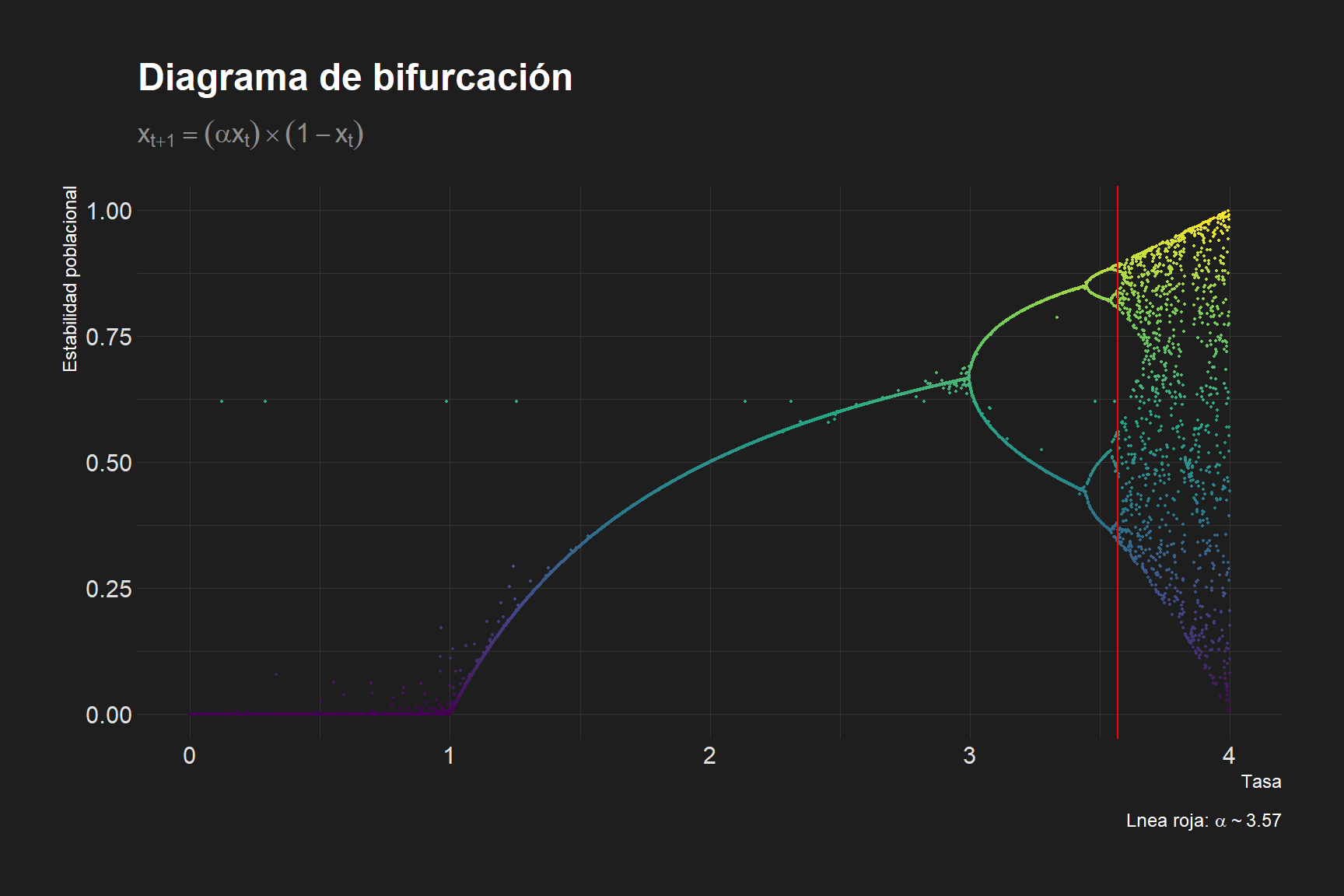
result_simulation %>%
ggplot(aes(x = rate, y = pob, color = pob)) +
geom_point(size = 0.4) +
labs(x = "Tasa",
y = "Estabilidad poblacional",
title = "Diagrama de bifurcación",
subtitle = TeX(r'($x_{t+1}= (\alpha x_t) \times (1-x_t)$)'),
caption = TeX(r'(Lnea roja: $ \alpha \sim 3.57$)')) +
geom_vline(xintercept = 3.57, color = "red", size = 0.4) +
scale_color_viridis_c() +
theme_modern_rc() +
theme(legend.position = "none")