Contenido

1. Información general (requisitos previos, bibliotecas, etc).
2. Análisis inicial de los datos. Como el objetivo principal del documento es entrenar un modelo de árbol de decisión con R, el análisis inicial incluye sólo una parte exploratoria y algunas pruebas estadísticas.
3. Entrenamiento de modelo por defecto con rpart.
4. Ajuste de hiperparámetros con la biblioteca caret. La métrica para evaluar el desempeño predictivo de los modelos es el área bajo la curva ROC.
5. Material complementario.
6. Recursos de información.

Requisitos previos

Instalar las bibliotecas rpart y rpart.plot para entrenar y gráficar modelos basados en árboles.
Instalar la biblioteca caret.
Descargar datos para ejemplo desde la página openML. La base de datos proporciona información de personas perfiladas con riesgo crediticio bueno o malo.
Bibliotecas complementarias: para visualizaciones ggplot2, jcolors y hrbrthemes, para manejo de datos dplyr y para métricas de error y/o precisión Metrics y pROC.

Bibliotecas

Código

library(dplyr)
library(ggplot2)
library(jcolors)
library(hrbrthemes)
library(rpart)
library(rpart.plot)
library(caret)
library(Metrics)
library(pROC)

Descripción de variables

Además de la variable respuesta class, se cuenta con las siguientes 20 variables.

Datos

Se importan los datos y se aplica la función mutate_if() para eliminar las comillas simples (’’) que están presentes en las variables tipo texto (character). A continuación sólo se muestran 5 variables (columnas) con 10 observaciones. La variable class es nuestro target o variable respuesta.

Código

data <- data.table::fread(file = "data/dataset_31_credit-g.csv") %>% 
  mutate_if(is.character, funs(gsub("'", "", .)))
head(data[1:10, c(1, 5, 10, 15, 21)], n = 10L) # Imprimiendo sólo 5 columnass

Dimensión de la base de datos:

Código

dim(data)

[1] 1000   21

Distribución de variable respuesta

Código

data %>% 
  ggplot(mapping = aes(x = class, fill = class)) +
  geom_bar(color = "black") + 
  scale_fill_manual(values = c("#5A5156", "#F6222E")) +
  theme_ipsum() +
  theme(legend.position = "none")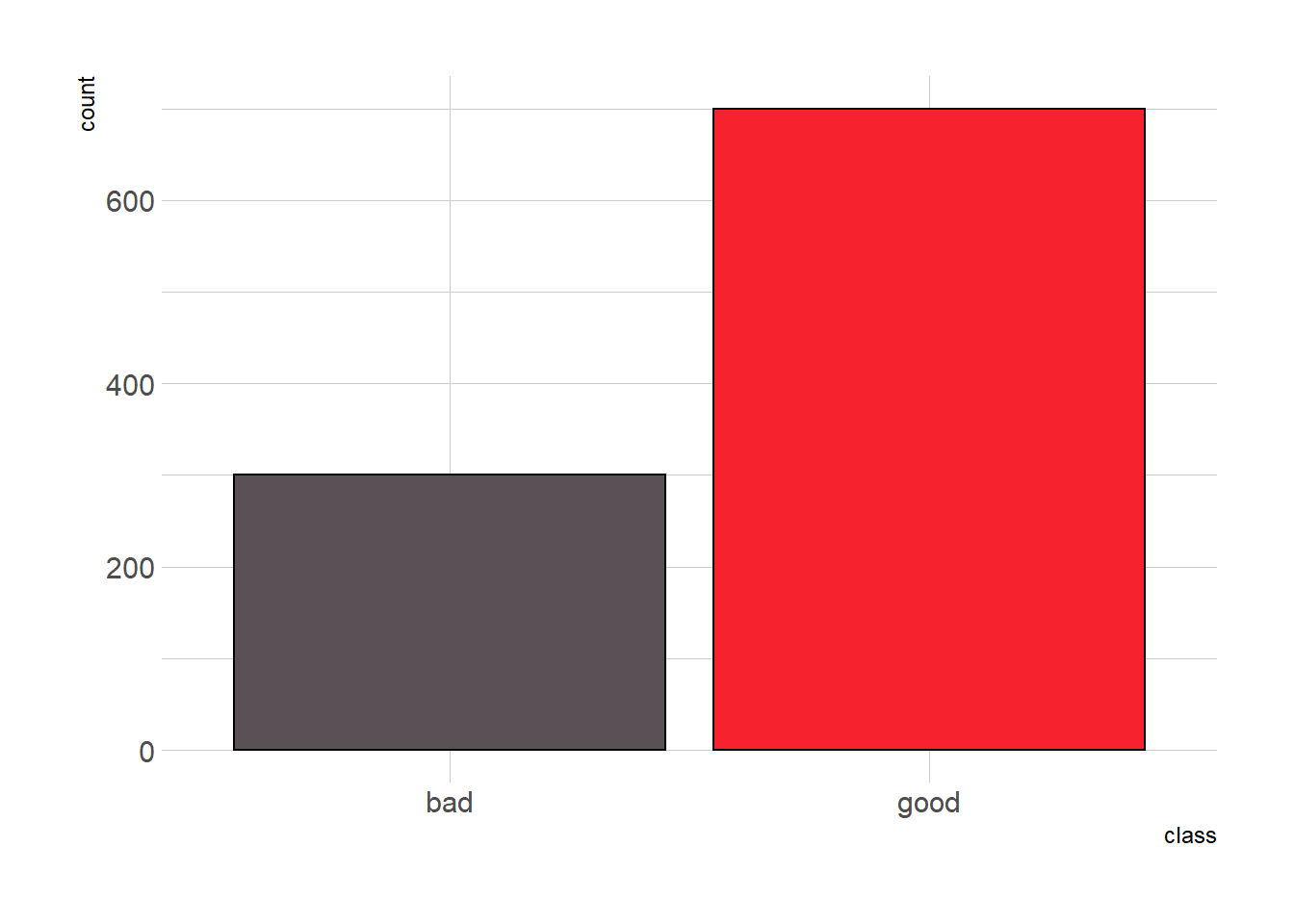

Exploratorio

Distribución de edad por variable objetivo: se puede apreciar que la edad promedio de los clasificados como “buenos” es más alta, además, los clasificados como “malos” en su mayoría son personas entre 20 y 30 años de edad.

Código

data %>% 
  ggplot(mapping = aes(x = class, y = age, fill = class)) +
  geom_violin() +
  geom_boxplot(color = "#E4E1E3", width = 0.1, show.legend = FALSE)  +
  stat_summary(fun.y = mean, color = "#E4E1E3", pch = 17) +
  scale_fill_manual(values = c("#5A5156", "#F6222E")) +
  theme_ipsum() +
  theme(legend.position = "none") +
  labs(caption = "El triángulo representa el promedio."))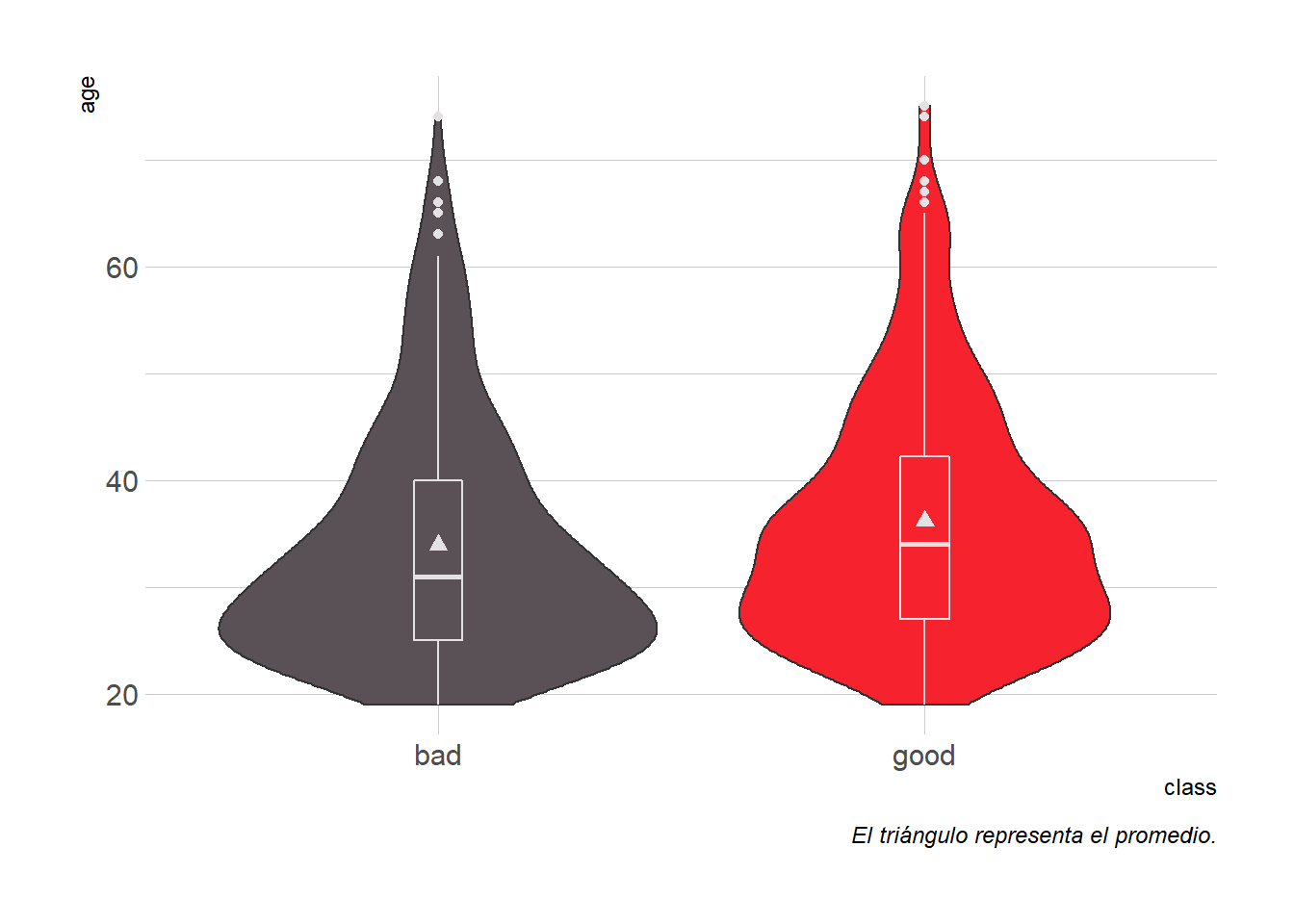

Propósitos de crédito más frecuentes: la distribución de personas clasificadas como buenas o malas cuando el propósito es vehículo, discrepa bastante entre la opción de nuevo o usado. En vehículos usados la gran mayoría son clasificados como “buenos”, sin embargo, cuando se trata de vehículos nuevos, la distribución es similar, lo que permite inferir que es más probable que una persona se comporte como mal pagador en créditos para vehículo nuevo respecto a créditos para vehículos usados. También se podría intuir que cuando se trata de créditos para educación es igual de probable que la persona sea clasificada como “bueno” o “malo”.

Código

data %>% 
  group_by(class, purpose) %>% 
  count() %>% 
  ggplot(mapping = aes(x = reorder(purpose, n), y = n, fill = class)) +
  geom_col(color = "#E4E1E3", position = "dodge") +
  scale_fill_manual(values = c("#5A5156", "#F6222E")) +
  labs(x = "Purpose") +
  theme_ipsum() +
  theme(legend.position = "top",
        axis.text.x = element_text(angle = 45, hjust = 1))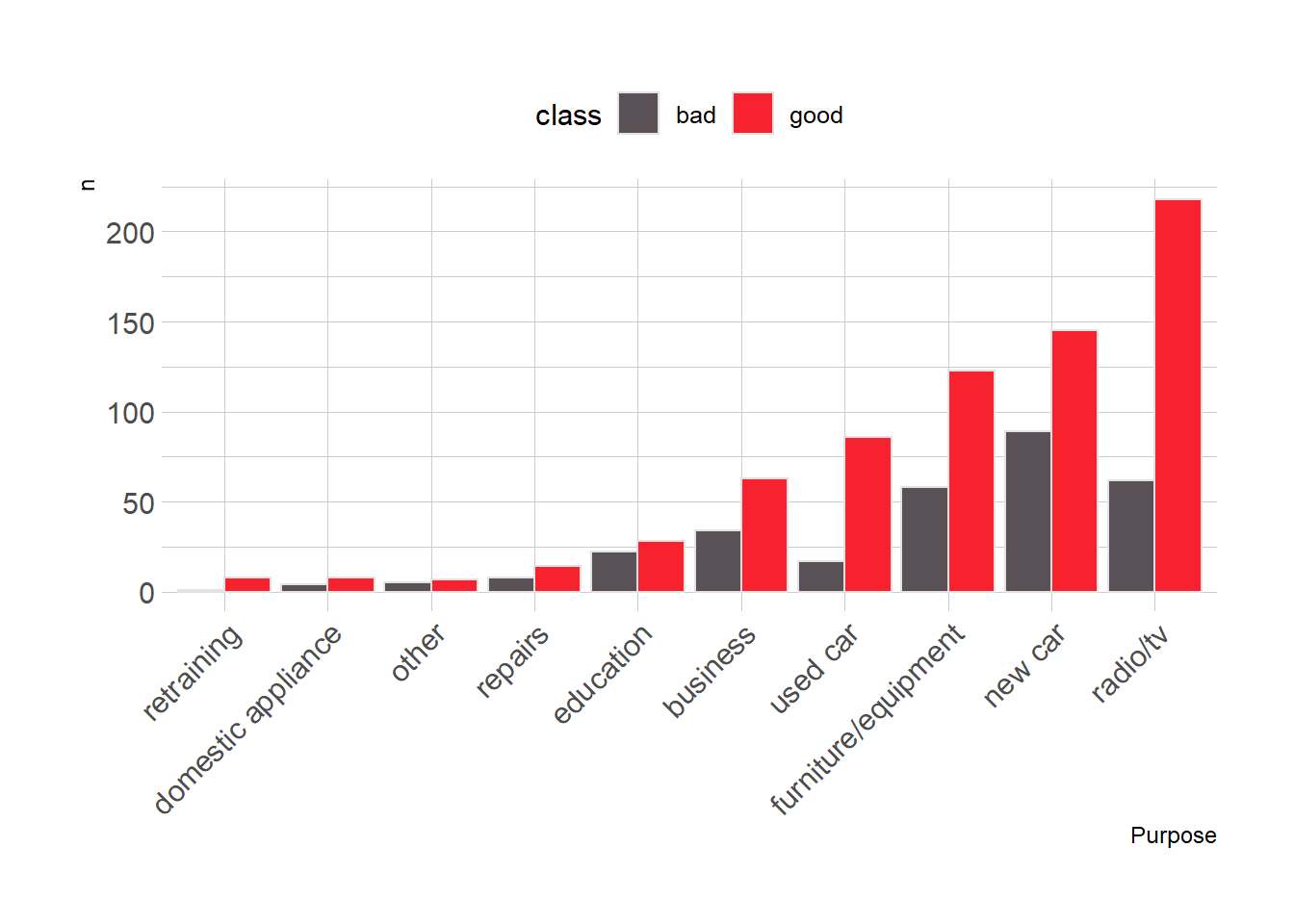

Inferencia

Análisis de varianza: en vista de la discrepancia que se observa en la distribución de las edades para personas clasificadas como “buenas” o “malas”, realizo el análisis de varianza para contrastar si dichas diferencias son estadísticamente significativas. Nota: aunque nuestra variable respuesta es class, en este caso actúa como “predictora” o fuente de variación.

Código

myAnova <- aov(age ~ class, data = data)
summary(myAnova)

             Df Sum Sq Mean Sq F value  Pr(>F)   
class         1   1074  1073.5   8.357 0.00393 **
Residuals   998 128198   128.5                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

El resultado de la prueba muestra que existe evidencia estadísticamente significativa (p=0.00393) para considerar que la variación de la edad entre ambos grupos es diferente.

Árboles de decisión

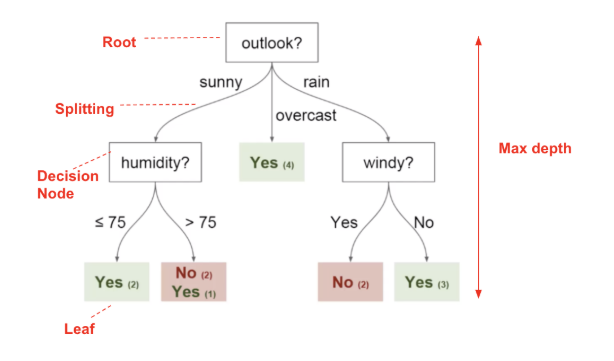
Generalidades

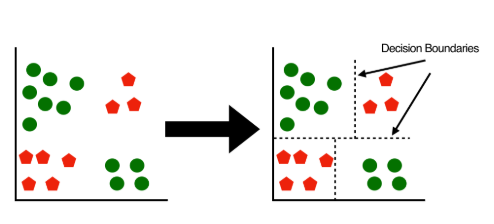
Los árboles de decisión se pueden utilizar para problemas de regresión y clasificación.
Se pueden definir como una estructura jerárquica que busca particionar el espacio de características e identificar subconjuntos representativos. Desde la parte superior a inferior cada árbol tiene nodo raíz, nodos de decisión o internos y nodos hojas o terminales, los dos primeros se generan con base en reglas binarias. Mayor grado de pureza es la recompensa que busca el algoritmo al particionar el espacio inicial en subregiones, en ese orden de ideas el objetivo siempre será particionar los datos en nodos que sean lo más puros posible, sin embargo, matemáticamente es más fácil medir la impureza de una región específica, proporcionando una idea de qué tan heterogéneas son las clases en ese nodo; una métrica de uso común en problemas de clasificación para medir la impureza es el índice GINI, donde valores bajos indican mayor grado de pureza. Además del índice GINI también es posible utilizar otras métricas como la ganancia de información o la entropía.
Ventajas:
- Fácil de interpretar (sujeto a la profundidad).
- No requieren estandarización o normalización de variables predictoras numéricas.
- Permiten manipular variables categóricas sin necesidad de aplicar codificaciones tipo one-hot o variables dummy.
- Requieren poco preprocesamiento de datos.
- Permiten valores ausentes (NA).
- Permite relaciones no lineales.
Desventajas:
- Si no se controla adecuadamente la profundidad del árbol existe alta probabilidad de incurrir en sobreajuste (overfitting).
- Alta varianza, pequeños cambios en los datos pueden arrojar resultados muy diferentes.
Hiperparámetros: aunque ejecutar la función rpart() con valores predeterminados puede ser una buena estrategia para iniciar, siempre estaremos interesados en ajustar determinados parámetros que nos permitan obtener mejor rendimiento predictivo. La función rpart.control() permite controlar manualmente otras opciones. Dentro los hiperparámetros más importantes en árboles de decisión están los siguientes:
- Mínimo número de observaciones para generar una partición. En la biblioteca rpart lleva el nombre de minsplit y su valor por defecto es 20.
- Máxima profundiad del árbol. En la biblioteca rpart lleva el nombre de maxdepth y su valor predeterminado es 30. Este parámetro es de alta relevancia para evitar el sobreajuste.
- Parámetro de complejidad. En la biblioteca rpart lleva el nombre de cp y su valor por defecto es 0.01. Este parámetro sirve al propósito de penalizar y contolar el tamaño del árbol, valores bajos indican árboles de mayor complejidad, es decir, mayor número de divisiones. La función rpart() internamente ejecuta validación cruzada 10 veces para estimar el valor óptimo de cp, es posible acceder a dicho resultado a través de la función plotcp() que permitirá facilmente determinar el valor adecuado para este parámetro. Cuando se tiene el valor óptimo de cp será posible “podar” el árbol para que el modelo sea optimizado, dicho resultado es posible a través de la función prune().

Train - Test

Para entrenar el modelo inicialmente fracciono los datos en train y test con proporciones de 70 y 30%, respectivamente. Este proceso aunque es posible hacerlo manualmente con la función sample(), la función createDataPartition() del paquete caret agiliza el procedimiento. Para garantizar replicabilidad en los resultados se agrega la semilla.

Código

set.seed(1992)
idx <- createDataPartition(y = data$class, times = 1, p = 0.70, list = FALSE)
dataTrain <- data[idx, ]
dataTest <- data[-idx, ]

`rpart` default

Ajuste del modelo: en este caso se utilizan todas las variables predictoras para entrenar el modelo. Al imprimir el objeto que contiene el modelo podemos observar el conjunto de reglas que dan como resultado la estructura final del árbol. El método igualado a method = "class" indica que es un problema de clasificación, si fuese un problema de regresión el argumento tomaría el valor de method = "anova", aunque también permite otras opciones (consulte ?rpart o help("rpart")).

Código

modArbol0 <- rpart(class ~ ., data = dataTrain, method = "class")
modArbol0

n= 700 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

  1) root 700 210 good (0.3000000 0.7000000)  
    2) checking_status=<0,0<=X<200 385 168 good (0.4363636 0.5636364)  
      4) credit_history=all paid,no credits/all paid 51  14 bad (0.7254902 0.2745098)  
        8) savings_status=<100,100<=X<500 42   8 bad (0.8095238 0.1904762) *
        9) savings_status=500<=X<1000,no known savings 9   3 good (0.3333333 0.6666667) *
      5) credit_history=critical/other existing credit,delayed previously,existing paid 334 131 good (0.3922156 0.6077844)  
       10) duration>=27.5 77  30 bad (0.6103896 0.3896104)  
         20) purpose=domestic appliance,education,furniture/equipment,new car 39  10 bad (0.7435897 0.2564103) *
         21) purpose=business,other,radio/tv,repairs,used car 38  18 good (0.4736842 0.5263158)  
           42) checking_status=<0 19   7 bad (0.6315789 0.3684211) *
           43) checking_status=0<=X<200 19   6 good (0.3157895 0.6842105) *
       11) duration< 27.5 257  84 good (0.3268482 0.6731518)  
         22) purpose=domestic appliance,education,new car,retraining 83  41 good (0.4939759 0.5060241)  
           44) age< 35.5 42  13 bad (0.6904762 0.3095238)  
             88) credit_amount< 1392 20   1 bad (0.9500000 0.0500000) *
             89) credit_amount>=1392 22  10 good (0.4545455 0.5454545)  
              178) property_magnitude=life insurance,real estate 13   4 bad (0.6923077 0.3076923) *
              179) property_magnitude=car,no known property 9   1 good (0.1111111 0.8888889) *
           45) age>=35.5 41  12 good (0.2926829 0.7073171) *
         23) purpose=business,furniture/equipment,other,radio/tv,repairs,used car 174  43 good (0.2471264 0.7528736) *
    3) checking_status=>=200,no checking 315  42 good (0.1333333 0.8666667) *

Gráfico del modelo: la variable más importante y que da origen al nodo raíz es checking_status, que hace referencia al estado de la cuenta corriente. El historial crediticio, la duración del tiempo para pagar el crédito, el estado de la cuenta de ahorros y el propósito del crédito, también son factores determinantes. No tener suficiente capital en cualquiera de las dos cuentas, tener mal historial crediticio y además solicitar períodos de pago de alta duración, pueden ser características no deseables a la hora de solicitar un crédito.

Código

rpart.plot(modArbol0)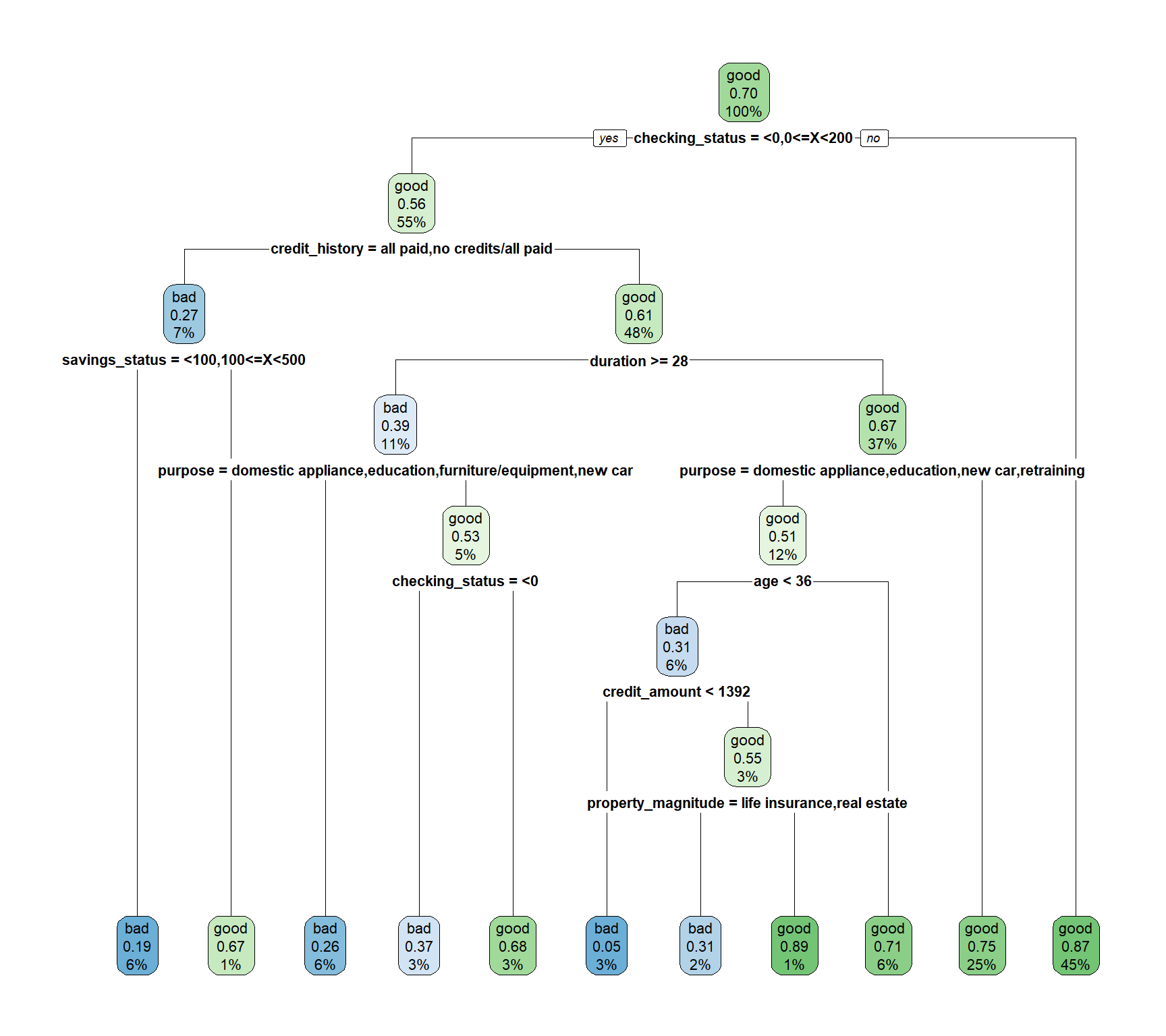

Matriz de confusión: el modelo por default tiene precisión promedio de 0.7167, con dificultades para clasificar de forma correcta los “malos”, es decir, que tiene baja especificidad.

Código

predichos_mod0 <- predict(object = modArbol0, newdata = dataTest, type = "class")
confusionMatrix(data = predichos_mod0, reference = as.factor(dataTest$class),
                positive = "good")

Confusion Matrix and Statistics

          Reference
Prediction bad good
      bad   31   26
      good  59  184
                                        
               Accuracy : 0.7167        
                 95% CI : (0.662, 0.767)
    No Information Rate : 0.7           
    P-Value [Acc > NIR] : 0.2873596     
                                        
                  Kappa : 0.2465        
                                        
 Mcnemar's Test P-Value : 0.0005187     
                                        
            Sensitivity : 0.8762        
            Specificity : 0.3444        
         Pos Pred Value : 0.7572        
         Neg Pred Value : 0.5439        
             Prevalence : 0.7000        
         Detection Rate : 0.6133        
   Detection Prevalence : 0.8100        
      Balanced Accuracy : 0.6103        
                                        
       'Positive' Class : good

Área bajo la curva:

Código

# Probabilidades predichas para la clase "good"
pred0 <- as.data.frame(predict(object = modArbol0,
                               newdata = dataTest, type = "prob"))$good

# Transformando respuesta a entero. A la clase "good" le agrego 1 y 
# a la clase "bad" le agrego 0.
target <- as.integer(as.factor(dataTest$class)) - 1

# AUC
Metrics::auc(actual = target, predicted = pred0)

[1] 0.7034392

Curva ROC: la función con la que obtengo el siguiente gráfico puede ser encontrada en mi Github.

Código

# Cargando funciónn
source("functions/myROC.R")

# Ver función myROC() al final en material complementario     
myROC(predichos = pred0, reales = target)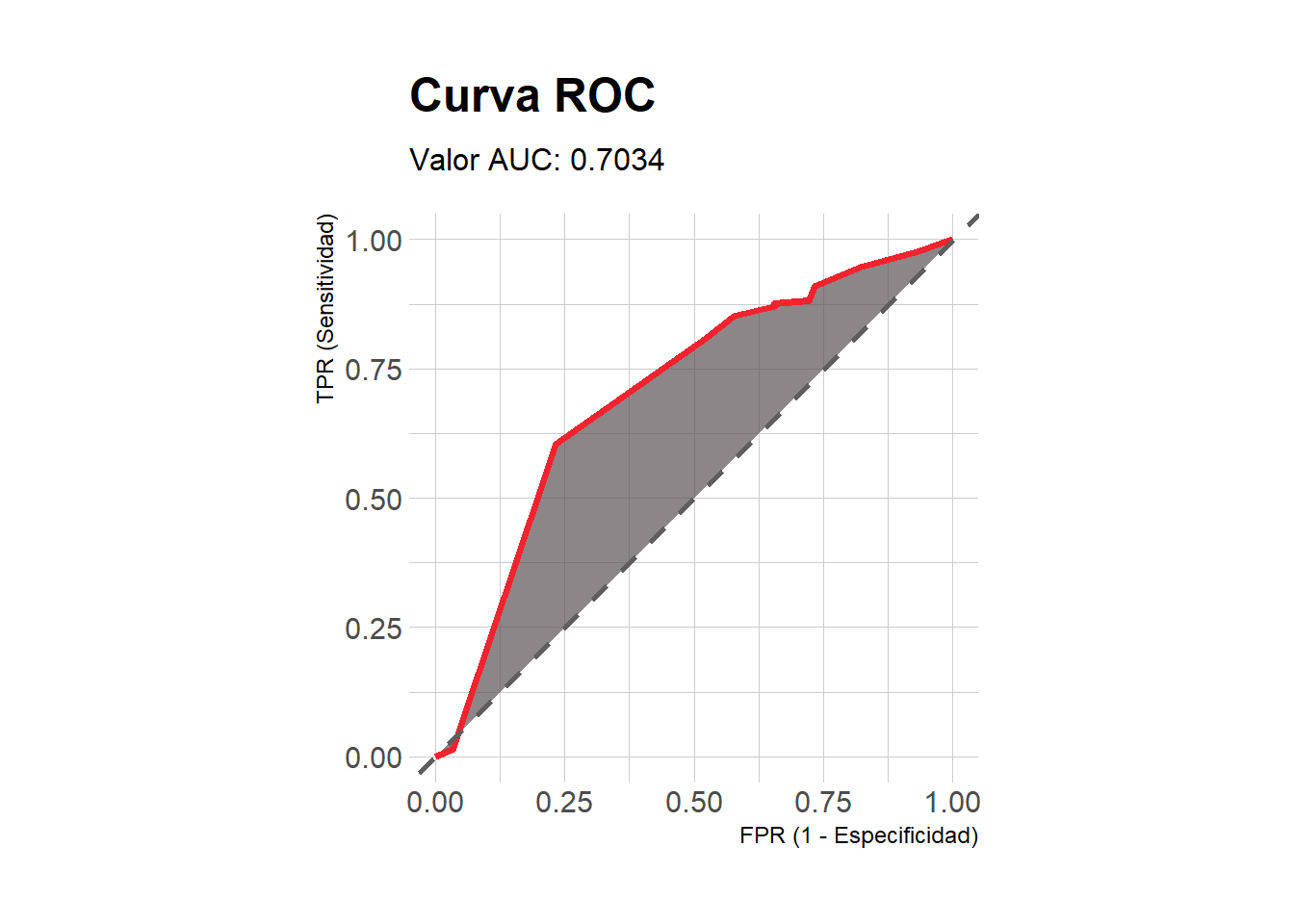

Parámetro de complejidad (CP):

Código

plotcp(modArbol0)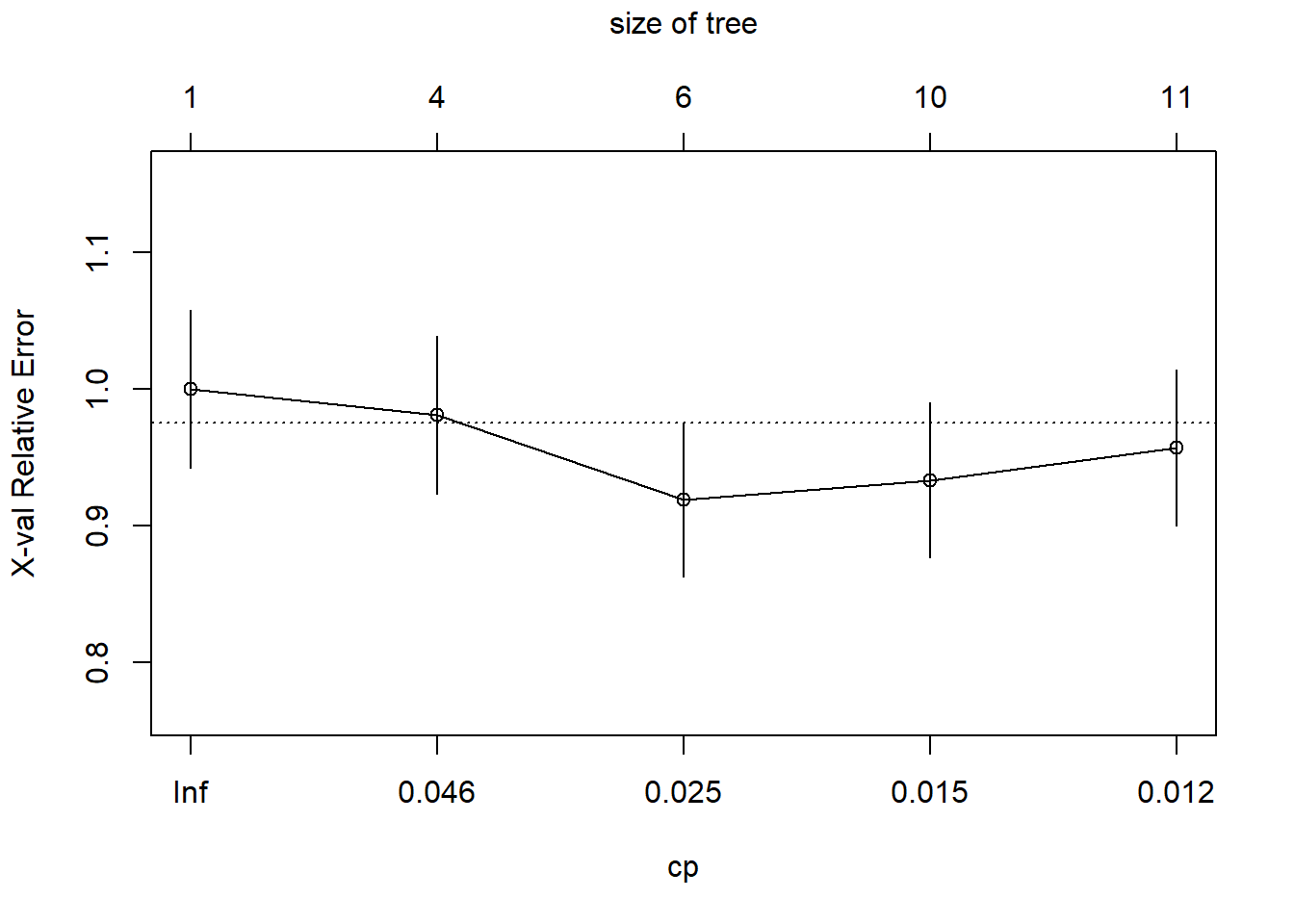

“Podando” el árbol: se elige el valor de cp = 0.025 por mostrar mejores resultados (bajo error).

Código

modArbol0_prune <- prune(tree = modArbol0, cp = 0.025)
modArbol0_prune

n= 700 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 700 210 good (0.3000000 0.7000000)  
   2) checking_status=<0,0<=X<200 385 168 good (0.4363636 0.5636364)  
     4) credit_history=all paid,no credits/all paid 51  14 bad (0.7254902 0.2745098) *
     5) credit_history=critical/other existing credit,delayed previously,existing paid 334 131 good (0.3922156 0.6077844)  
      10) duration>=27.5 77  30 bad (0.6103896 0.3896104) *
      11) duration< 27.5 257  84 good (0.3268482 0.6731518)  
        22) purpose=domestic appliance,education,new car,retraining 83  41 good (0.4939759 0.5060241)  
          44) age< 35.5 42  13 bad (0.6904762 0.3095238) *
          45) age>=35.5 41  12 good (0.2926829 0.7073171) *
        23) purpose=business,furniture/equipment,other,radio/tv,repairs,used car 174  43 good (0.2471264 0.7528736) *
   3) checking_status=>=200,no checking 315  42 good (0.1333333 0.8666667) *

Gráfico de árbol con “poda”:

Código

rpart.plot(modArbol0_prune)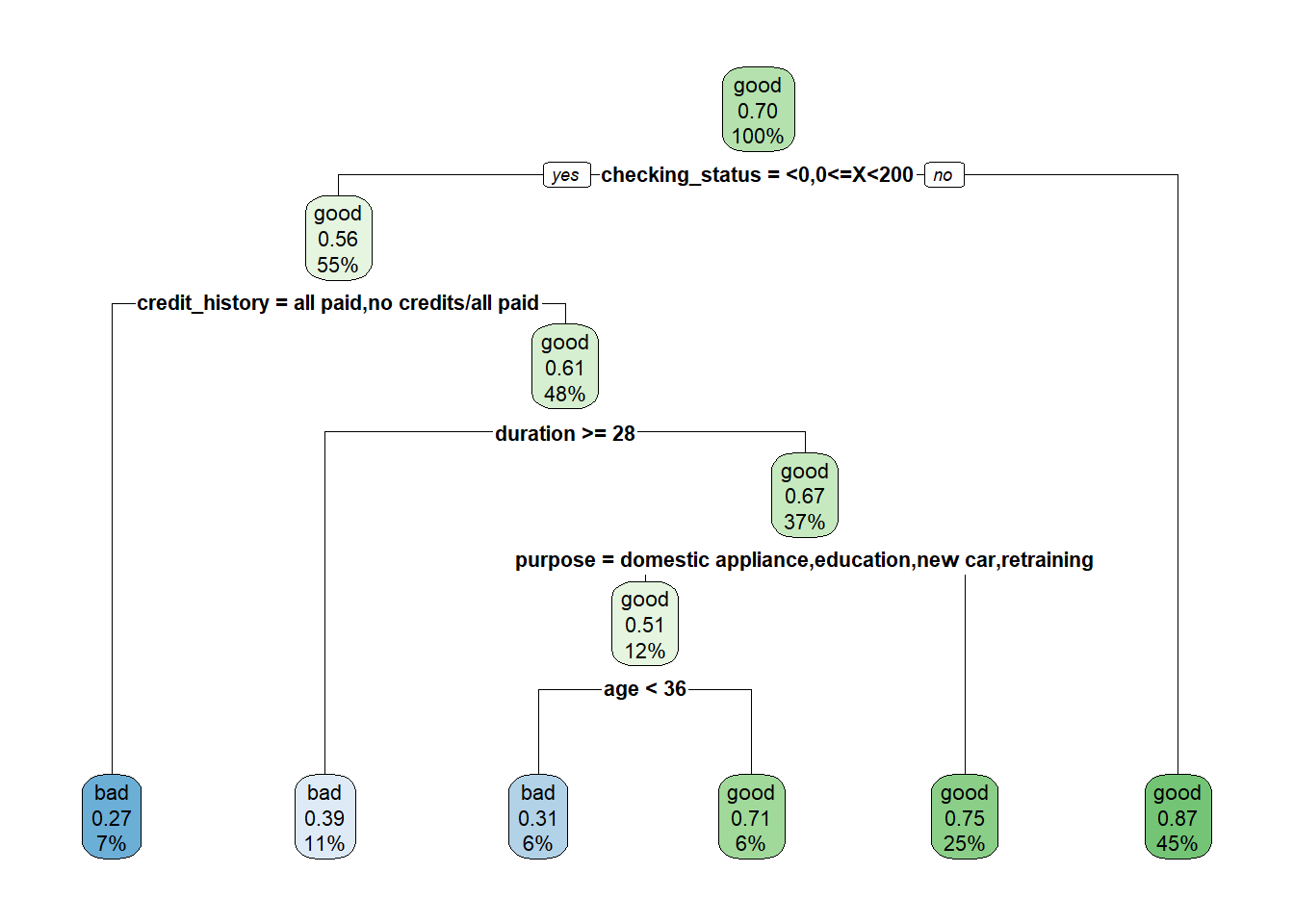

Matriz de confusión árbol con “poda”: respecto al árbol sin podar, la diferencia en precisión es muy pequeña (<0.01), sin embargo, la especificidad se aumenta de 0.3444 a 0.4556 con la “poda”, aunque la sensitividad haya reducido de 0.8762 a 0.8381.

Código

predichos_mod0_prune <- predict(object = modArbol0_prune, newdata = dataTest, type = "class")
confusionMatrix(data = predichos_mod0_prune, reference = as.factor(dataTest$class),
                positive = "good")

Confusion Matrix and Statistics

          Reference
Prediction bad good
      bad   41   34
      good  49  176
                                         
               Accuracy : 0.7233         
                 95% CI : (0.669, 0.7732)
    No Information Rate : 0.7            
    P-Value [Acc > NIR] : 0.2072         
                                         
                  Kappa : 0.3083         
                                         
 Mcnemar's Test P-Value : 0.1244         
                                         
            Sensitivity : 0.8381         
            Specificity : 0.4556         
         Pos Pred Value : 0.7822         
         Neg Pred Value : 0.5467         
             Prevalence : 0.7000         
         Detection Rate : 0.5867         
   Detection Prevalence : 0.7500         
      Balanced Accuracy : 0.6468         
                                         
       'Positive' Class : good

Área bajo la curva de árbol con “poda”:

Código

# Probabilidades predichas para la clase "good"
pred0_prune <- as.data.frame(predict(object = modArbol0_prune,
                                     newdata = dataTest, type = "prob"))$good

# AUC
Metrics::auc(actual = target, predicted = pred0_prune)

[1] 0.7203175

Curva ROC:

Código

# Ver función myROC() al final en material complementario     
myROC(predichos = pred0_prune, reales = target)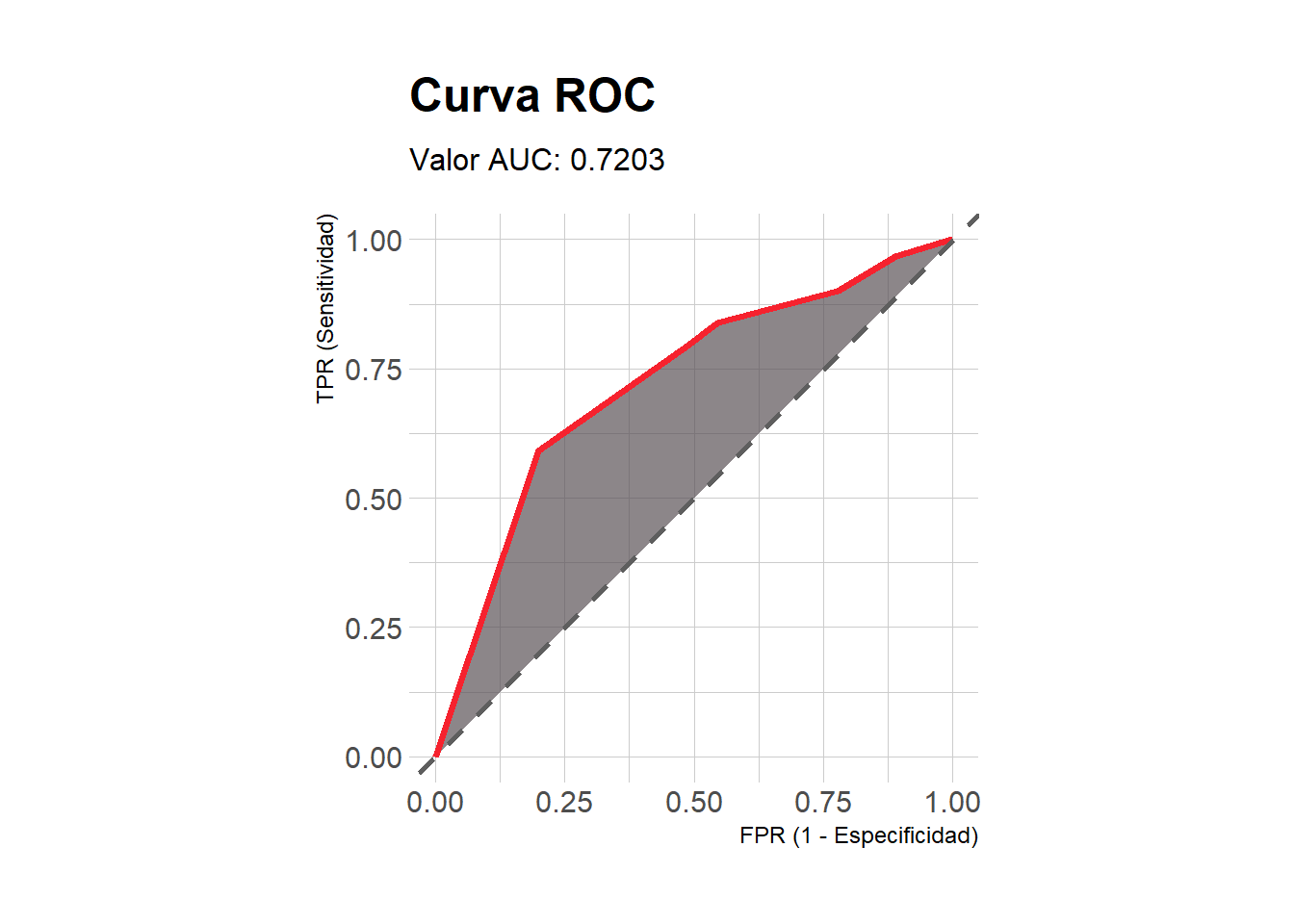

Tuning con caret

A diferencia de los parámetros que se “aprenden” duarante el entrenamiento del modelo, los hipeparámetros se definen previo al ajuste del mismo.
El ajuste de hiperparámetros se constituye como parte fundamental de la optimización del modelo.
La biblioteca caret proporciona un marco de trabajo unificado para entrenar y validar modelos de machine learning. En este caso, con caret podremos ajustar dos de los tres hiperparámetros mencionados anteriormente, el parámetro de complejidad y la profundidad del árbol. Las funciones trainControl() y train de la biblioteca caret facilitan el proceso.
- trainControl(): permite establecer la estrategia de validación, por ejemplo validación cruzada k-fold, validación cruzada repetida, bootstrapping, entre otras. Desde esta misma función también es posible determinar el método de búsqueda de hiperparámetros, que puede ser aleatoria o cuadrícula (grid). En este caso particular utilizo validación cruzada con repeticiones, con k = 5 y 3 repeticiones. El argumento summaryFunction = twoClassSummary permite computar las métricas necesarias (sensitividad y especificidad) para obtener ROC. Busque más ayuda con help("trainControl").
- train(): ajuste el modelo estableciendo la fórmula habitual en R, el método o algoritmo para entrenar, (lista de algoritmos en caret) los datos, la configuración para el entrenamiento (tcConrol = myControl) y la longitud de hiperparámetros a considerar en el entrenamiento (tuneLenth). Este último argumento dependerá de los hiperparámetros que estén disponibles en caret, aunque también es posible asignarlos manualmente a través de expand.grid(). Utilizar el método igualado a “rpart” permitirá optimizar el parámetro cp y utilizando “rpart2” es posible optimizar la máxima profundidad del árbol. Cuando se declara tuneLength = 5 se informa que el número máximo de profundidades a probar será 5, es decir, que al final existirán 5 resultados diferentes con el mismo algoritmo. Por último, se agrega la métrica que será utilizada para comparar los resultados de la validación cruzada.
Nota: como el procedimiento de validación cruzada implica muestreo aleatorio, es necesario asignar la semilla para garantizar replicabilidad de resultados.

Código

myControl <- trainControl(method = "repeatedcv",
                          number = 5,
                          repeats = 3,
                          classProbs = TRUE,  # Permite predecir probabilidades
                          summaryFunction = twoClassSummary) 
set.seed(1992)
modArbol_tune <- train(class ~ .,
                       method = "rpart2",
                       data = data,
                       trControl = myControl,
                       tuneLength = 5,
                       metric = "ROC")
modArbol_tune

CART 

1000 samples
  20 predictor
   2 classes: 'bad', 'good' 

No pre-processing
Resampling: Cross-Validated (5 fold, repeated 3 times) 
Summary of sample sizes: 800, 800, 800, 800, 800, 800, ... 
Resampling results across tuning parameters:

  maxdepth  ROC        Sens       Spec     
   3        0.7028968  0.3011111  0.8885714
   6        0.7138095  0.3244444  0.8880952
  11        0.7211151  0.3988889  0.8642857
  14        0.7213571  0.4055556  0.8623810
  18        0.7211746  0.3911111  0.8671429

ROC was used to select the optimal model using the largest value.
The final value used for the model was maxdepth = 14.

Se observa que la mejor profundidad es 14 con la mayor sensitividad aún cuando no tiene la mejor especificidad. A continuación la matriz de confusión en el conjunto de test muestra mejoras en la capacidad de detectar los clasificados como “malos”, ademas la precisión es notablemente superior.

Código

predichos_tune <- predict(object = modArbol_tune, newdata = dataTest, type = "raw")
confusionMatrix(data = predichos_tune, reference = as.factor(dataTest$class),
                positive = "good")

Confusion Matrix and Statistics

          Reference
Prediction bad good
      bad   52   29
      good  38  181
                                          
               Accuracy : 0.7767          
                 95% CI : (0.7253, 0.8225)
    No Information Rate : 0.7             
    P-Value [Acc > NIR] : 0.001839        
                                          
                  Kappa : 0.4526          
                                          
 Mcnemar's Test P-Value : 0.328393        
                                          
            Sensitivity : 0.8619          
            Specificity : 0.5778          
         Pos Pred Value : 0.8265          
         Neg Pred Value : 0.6420          
             Prevalence : 0.7000          
         Detection Rate : 0.6033          
   Detection Prevalence : 0.7300          
      Balanced Accuracy : 0.7198          
                                          
       'Positive' Class : good

Área bajo la curva el modelo evidentemente consigue mejores resultados respecto a los ajustados inicialmente, de tal manera que el ajuste de hiperparámetros ha logrado mejorar nuestras predicciones en datos que el modelo aún no ha visto. Posiblemente el hecho de ajustar la máxima profundidad sumado al uso de validación cruzada, permite que el modelo capture de mejor manera las relaciones subyacentes entre características.

Código

# Probabilidades predichas para la clase "good"
pred_tune <- as.data.frame(predict(object = modArbol_tune,
                                   newdata = dataTest, type = "prob"))$good

# AUC
Metrics::auc(actual = target, predicted = pred_tune)

[1] 0.7888624

Curva ROC:

Código

# Ver función myROC() al final en material complementario     
myROC(predichos = pred_tune, reales = target)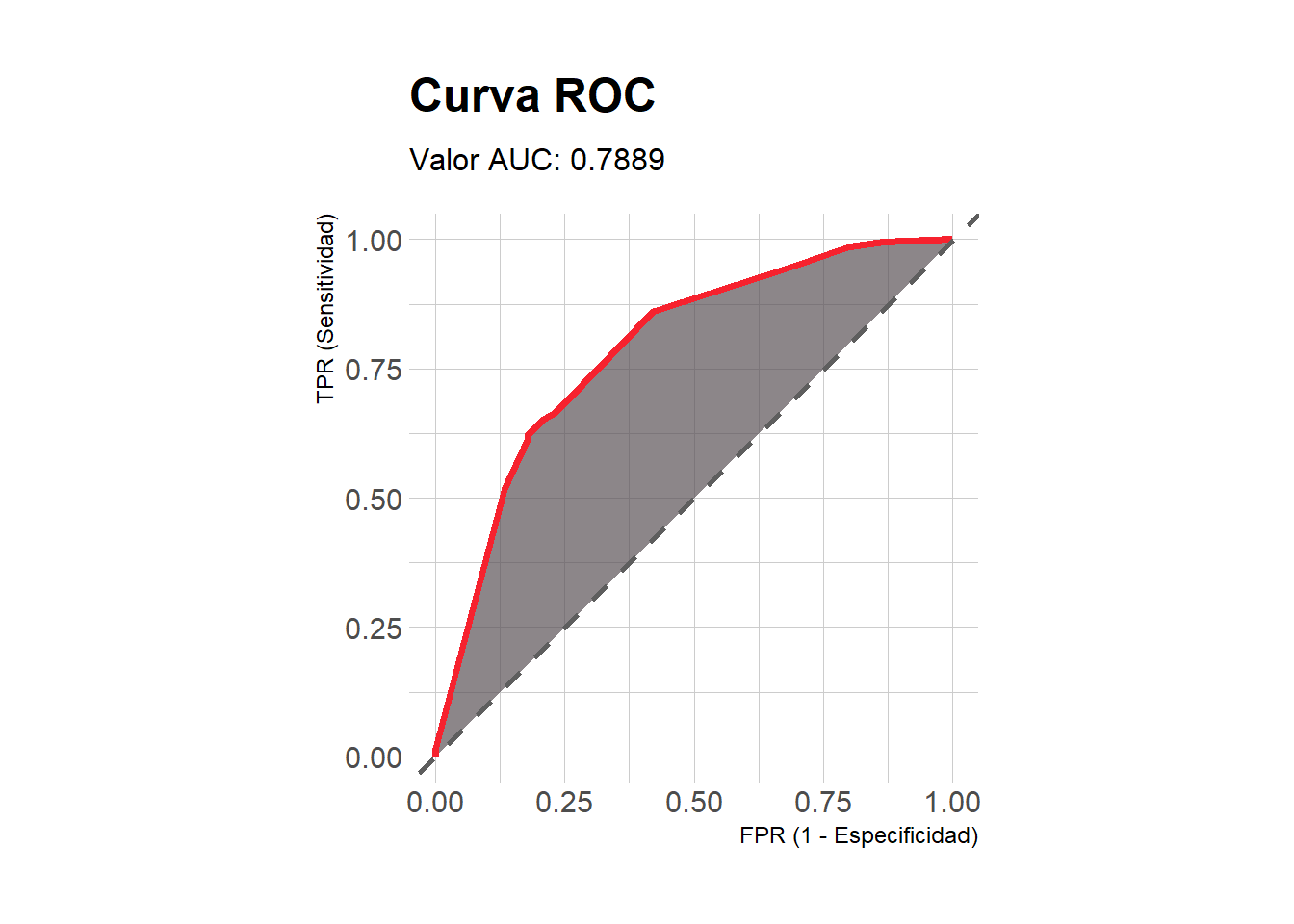

Complementario

Función `plot` + `caret`

La función plot() tiene un método específico para resultados obtenidos a través de caret, en este caso muestra el gráfico del hiperparámetro de interés, la máxima profundidad del árbol vs la curva ROC en el eje Y, tratando de evidenicar el valor óptimo.

Código

plot(modArbol_tune)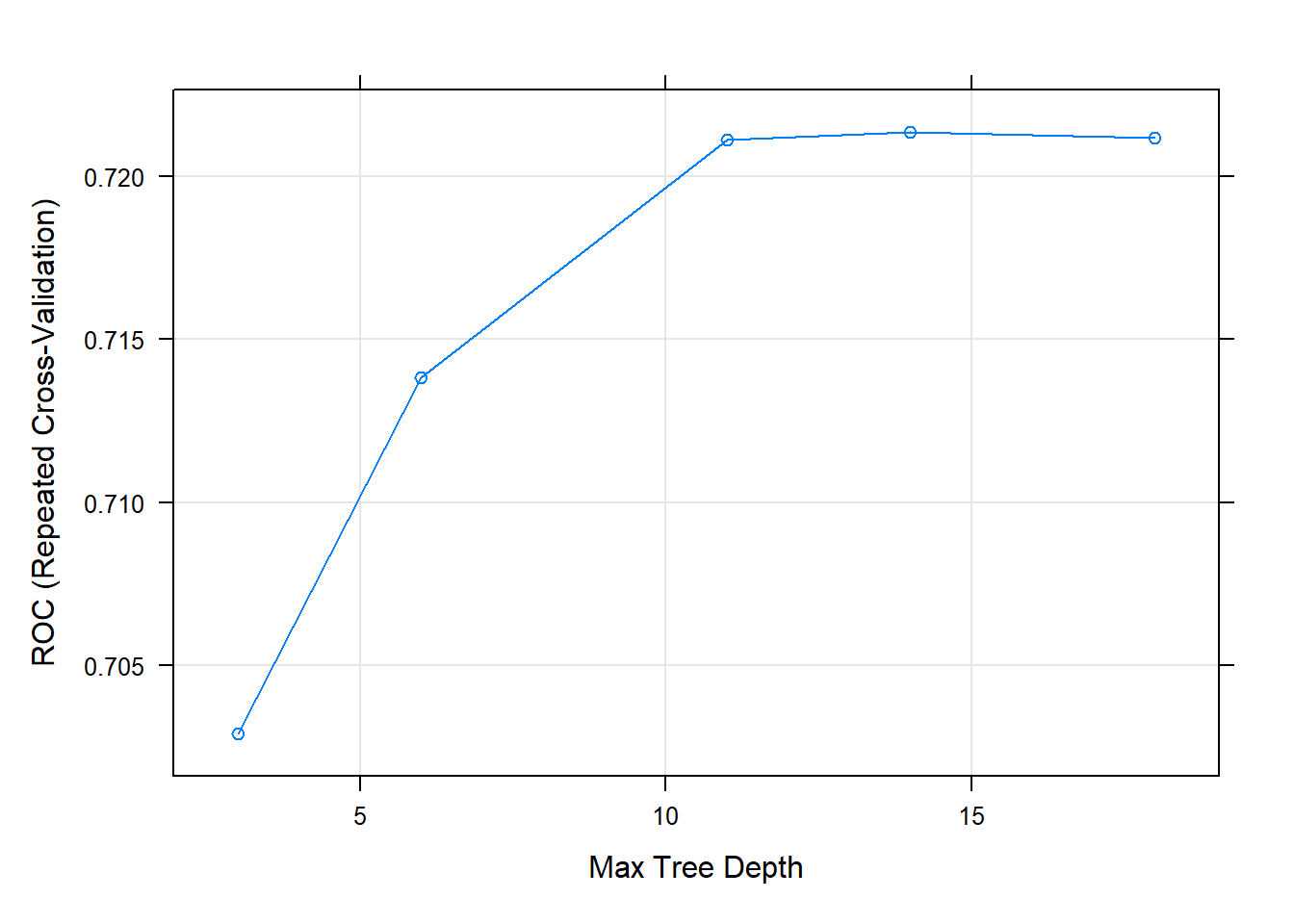

Gráfico interactivo con `visNetwork`

La biblioteca visNetwork permite crear gráficos interactivos para objetos de la clase rpart. A manera de ejemplo se presenta el gráfico para el árbol de decisión con poda. Recuerde que es interactivo y puede manipularlo con el mouse.

Código

library(visNetwork)
visTree(modArbol0_prune, 
        main = "Árbol con poda"", width=="100%"",
        height = "800px",  edgesFontSize = 14, nodesFontSize = 16,)

Función `myROC()`

Es necesario tener cargadas las bibliotecaS dplyr, ggplot2, hrbrthemes, Metrics y pROC para ejecutar la función.

Código

myROC <- function(predichos, reales) {
  suppressMessages(suppressWarnings(library(dplyr)))
  suppressMessages(suppressWarnings(library(ggplot2)))
  suppressMessages(suppressWarnings(library(pROC)))
  suppressMessages(suppressWarnings(library(Metrics)))
  x = roc(reales, predichos)
  df = data_frame(TPR = x$sensitivities,
                  FPR = 1 - x$specificities)
  gg = df %>%
    ggplot(aes(x = FPR, ymin = 0, ymax = TPR)) +
    geom_polygon(aes(y = TPR), fill = "#5A5156", alpha = 0.7) +
    geom_path(aes(y = TPR), col = "#F6222E", size = 1.3) +
    geom_abline(
      intercept = 0,
      slope = 1,
      color = "gray37",
      size = 1,
      linetype = "dashed"
    ) +
    theme_ipsum() +
    coord_equal() +
    labs(
      x = "FPR (1 - Especificidad)",
      y = "TPR (Sensitividad)",
      title = paste0("Curva ROC"),
      subtitle = paste0(
        "Valor AUC: ",
        Metrics::auc(actual = reales,
                     predicted = predichos) %>% round(4)
      )
    )
  return(gg)
}

Contenido

Requisitos previos

Bibliotecas

Descripción de variables

Datos

Distribución de variable respuesta

Exploratorio

Inferencia

Árboles de decisión

Generalidades

Train - Test

rpart default

Tuning con caret

Complementario

Función plot + caret

Gráfico interactivo con visNetwork

Función myROC()

Recursos de información

`rpart` default

Función `plot` + `caret`

Gráfico interactivo con `visNetwork`

Función `myROC()`